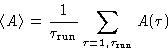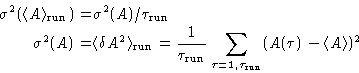Next: Hints for Using Program
Up: Appendix: Some Advice for
Previous: Appendix: Some Advice for
Williams and Holland's Law:
If enough data is collected, anything may be proven by
statistical methods.
Suppose we are analyzing the set of configurations, produced in either
MC or MD simulations. The total number of configurations is
 The time average of a property A is then
The time average of a property A is then
| 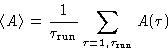 |
(1) |
If each 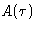 were statistically independent of the others,
the variance of the mean would simply be:
were statistically independent of the others,
the variance of the mean would simply be:
| 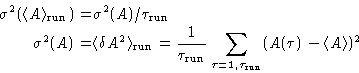 |
(2) |
and 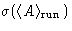 gives the estimated error in average.
But usually the data produce in MD and MC simulations are
correlated. As a limiting case we can assume, that our set of
gives the estimated error in average.
But usually the data produce in MD and MC simulations are
correlated. As a limiting case we can assume, that our set of
 configurations actually consists of blocks of
configurations actually consists of blocks of 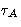 identical values (Jacucci and Rahman, 1984,
identical values (Jacucci and Rahman, 1984, 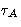 corresponds to
the correlation time in the MD simulations). Then
corresponds to
the correlation time in the MD simulations). Then
| 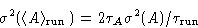 |
(3) |
To estimate the real error bars we split our data in blocks, varying
the block length 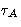 , calculate the block averages
, calculate the block averages
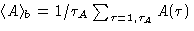 and then estimate
the variance, using these block averages:
and then estimate
the variance, using these block averages:
| 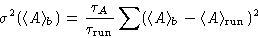 |
(4) |
As the block size increases, block averages become less and less
correlated, and 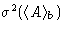 becomes proportional to the
number of blocks, or inversely proportional to
becomes proportional to the
number of blocks, or inversely proportional to 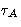 . This means,
that the value
. This means,
that the value 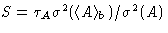 becomes
independent of
becomes
independent of 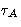 . Each S-th configuration of all produced
can be taken as a set of uncorrelated configurations. Thus the error
estimate should be based on the
. Each S-th configuration of all produced
can be taken as a set of uncorrelated configurations. Thus the error
estimate should be based on the 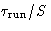 configurations, and
not
configurations, and
not  itself. That is why efficient MC algorithms are
developed to produced less correlated configurations in the same total
number of MC steps.
itself. That is why efficient MC algorithms are
developed to produced less correlated configurations in the same total
number of MC steps.



Next: Hints for Using Program
Up: Appendix: Some Advice for
Previous: Appendix: Some Advice for
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Dec 2 20:15:24 EST 1997
![]()
![]()
![]()
![]() The time average of a property A is then
The time average of a property A is then