Next: Fortran Code
Up: Molecular Dynamics II
Previous: Molecular Dynamics II
- Temperature:
- As the MD simulations are performed in the
microcanonical ensemble, temperature is not set, it is
obtained from the simulations. For the three-dimensional case:
| 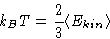 |
(1) |
- Pressure:
- Same way as in the MC using the virial formula.
| 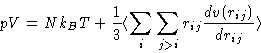 |
(2) |
- Structural Information:
- Can also be calculated exactly as in
the Monte Carlo simulations. Exactly same code for g(r) can be
used.
- Diffusion coefficient:
- This is what cannot be obtained from
Monte Carlo. The easiest way to calculate it from MD is by
Einstein relation:
| 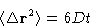 |
(3) |
The trajectory, obtained in the MD run, gives 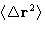 as
a function of t. It is plotted, and the tangent of the linear fit
gives diffusion coefficient. The algorithm:
as
a function of t. It is plotted, and the tangent of the linear fit
gives diffusion coefficient. The algorithm:
- 1.
- Configurations (snapshots) are saved every n steps during the MD run
- 2.
- The whole system trajectory is read by a separate
program into the array
![[*]](/icons/foot_motif.gif) x(k,ishot,ipart) that stores
k-th (x and y) coordinate of the particle
ipart at the ishot's frame saved.
x(k,ishot,ipart) that stores
k-th (x and y) coordinate of the particle
ipart at the ishot's frame saved.
- 3.
- The mean squared displacement is averaged over the particles and
over the initial configurations (see Code Example (8)).
- Time-correlation functions and spectra:
- Calculated exactly like
diffusion coefficient. We average over the particles and initial
conditions The Fourier transforms of different time correlation
functions are compared with spectroscopic experiments:
- Dipole correlations are relevant for the Dielectric
and Infra-red or Raman spectroscopy
- Orientation correlations of the C-H bonds can be measured
by the proton NMR
- etc.



Next: Fortran Code
Up: Molecular Dynamics II
Previous: Molecular Dynamics II
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Nov 26 01:51:43 EST 1997
![]()
![]()
![]()