


Next: Random Force and Its
Up: Time Correlation Functions. Random
Previous: Time Correlation Functions. Random
Subsections
We applied Fourier transform for space-dependent problems--and we were
successful. Let us do the same for time-dependent problems:
| 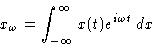 |
(1) |
Inverse transform:
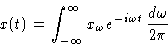
The product of x's is
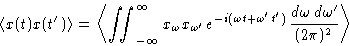
Or, since only x's are random,
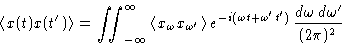
Symmetry with respect to time: 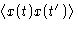 depends only on
t-t'. This means that in the integral
depends only on
t-t'. This means that in the integral 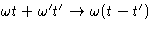 . This means that
. This means that 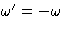 .
.
- Conclusion:
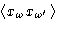 should be
proportional to
should be
proportional to 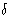 -function
-function 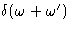
- Definition:
- Let
| 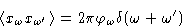 |
(2) |
Then
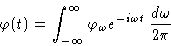
We see that 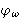 is indeed the Fourier transform of
is indeed the Fourier transform of
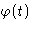 . This is exactly the function measured in inelastic
scattering, relaxation experiments (NMR, ESR, dielectric spectroscopy,
shear rheometry,...). Inverse:
. This is exactly the function measured in inelastic
scattering, relaxation experiments (NMR, ESR, dielectric spectroscopy,
shear rheometry,...). Inverse:
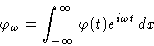
If t=0, we obtain
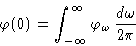
But 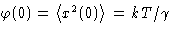 . We obtained:
. We obtained:
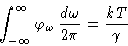
We obtained
for
correlation function
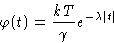
Take Fourier transform:
| 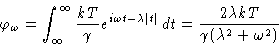 |
(3) |
This is a Lorentzian!
Relaxation with one characteristic time is Lorentzian.
Many characteristic times--more complex formulae.
Consider a large particle surrounded by small particles (a colloidal
particle among molecules). Equation for average velocity:
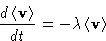
with friction coefficient 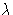 . For a spherical particle
with radius r and mass m in liquid with viscosity
. For a spherical particle
with radius r and mass m in liquid with viscosity 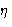
| 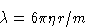 |
(4) |
The average square![[*]](/icons/foot_motif.gif)
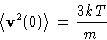
We immediately obtain autocorrelation function:
- In the real time:
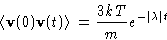
- After Fourier transform:
| 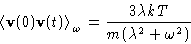 |
(5) |
Equations (3) and (5) are special cases of
fluctuation-dissipation theorem.
In particular, if 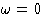
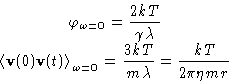
Consider particles with concentration c. Diffusion equation with
diffusion coefficient D:
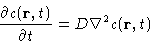
Fourier transform in space:
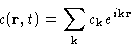
We obtain:
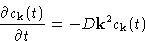
Let us now consider equilibrium. In equilibrium the fluid is
homogeneous. For 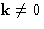 :
:
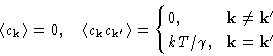
with 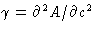 .
.
We immediately obtain:
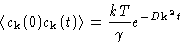
Or, in Fourier space
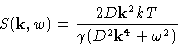
This is dynamic structure factor.



Next: Random Force and Its
Up: Time Correlation Functions. Random
Previous: Time Correlation Functions. Random
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 28 22:16:24 EST 1997
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
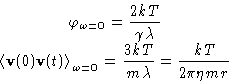
![]()
![]()
![]()
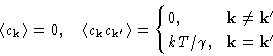
![]() .
.![]()
![]()