Subsections

• Gibbs Postulate
• Averaging and Ergodicity
• Entropy
• Thermodynamic limit
• Distribution Function

Time Evolution and Ergodicity

Gibbs Postulate

Trajectory--a line in phase space. Many-body systems: a complex entangled trajectory. Assumption: after long time the system ``forgets'' the initial conditions. Probability of each state does not depend on where we started!

What can it depend upon? Energy, total momentum, total volume,...

Microcanonical Ensemble:

Closed system $\Rightarrow$ all states have same energy, momentum,...

Gibbs Postulate:

All states in microcanonical ensemble are equivalent. They have the same probability to occur.

Averaging and Ergodicity

Two ways of averaging:

1.

I take one system and observe it for a long time (time averaging) :  

$$\left\langle f(p,q)\right\rangle_{\tau} = \lim_{\tau \right... ...infty}\frac{1}{\tau}\int_0^{\tau} f\bigl(p(t),q(t)\bigr)\,dt$$ (1)

2.

I take many systems from my ensemble (i.e. with same energy) and observe them all in one time (ensemble average):  

$$\left\langle f(p,q)\right\rangle_E = \frac{1}{\Omega} \int_{E=E_0} f(p,q)\, dp^N\,dq^N$$ (2)

with  

$$\Omega = \int_{E=E_0} dp^N\,dq^N$$ (3)

Ergodicity hypothesis: ensemble average is equal to time average.

$$\left\langle f(p,q)\right\rangle_\tau = \left\langle f(p,q)\right\rangle_E$$

Is ergodic hypothesis alway correct?

Gibbs postulate: yes.

But how large should be $\tau$ in (1) for the limit to work? What happens if it is a year? Twenty years? The mountains flowed down at Thy presence , but we are mortals....

Examples: water is liquid at frequencies $\approx1\,\mathrm{Hz}$, but solid at $10^{12}\,\mathrm{Hz}$. Window panes flow in hundred years...

Ergodic systems:

$\tau$ is small, and ergodicity works. Gases, liquids, crystals.

Non-ergodic systems:

$\tau$ is large, and we cannot wait for equilibrium. Glasses.

The same system can be both ergodic and non-ergodic depending on your time scale. Polymers.

Computer simulations: is the simulated system ergodic? Do we study its equilibrium or transient features?

Entropy

Each system in the ensemble is a point in the phase space. How many points are there?

Answer:

• Discrete space--just count them!
• Continuous space: measure the volume! Number of states

  $$W=\mathit{const}\times\text{Volume of phase space}$$

  The $\mathit{const}$ cannot be obtained in classical statistics. Quantum answer:

  $$\mathit{const}= \frac{1}{(2\pi\hbar)^{3N}}$$

Geometric interpretation: cell model

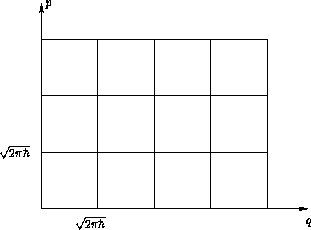
Entropy:  

$$S = k \ln W$$ (4)

Boltzmann constant: $k=1.38\times10^{-23}\,\mathrm{J/K}$

Thermodynamic limit

Suppose we increase the volume of our system V and the number of particles N.

Thermodynamic limit ($\text{T-limit}$):

$N\to\infty$, $V\to\infty$,and $N/V=\mathit{const}$. This limit is always taken!

Intensive variables:

A variable A is intensive if

$$\lim_{\text{T-limit}} A = \mathit{const}$$

Examples: temperature, pressure, density, concentration,...

Extensive variables:

A variable A is intensive, if

$$\lim_{\text{T-limit}} A = \infty, \lim_{\text{T-limit}} A/V = \mathit{const}$$

Examples: number of particles, volume, energy,...

Entropy of two non-interacting subsystems:

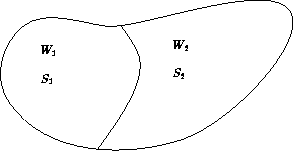
The total number of states:

$$W = W_1\times W_2$$

Entropy:

S = S₁ + S₂

Thermodynamic limit: many weakly interacting parts!

Entropy is an extensive quantity

Distribution Function

Let $\rho(p,q)$ be the probability to meet the given state in the ensemble. Ensemble averaging:

$$\left\langle f(p,q)\right\rangle_E = \int \rho(p,q) f(p,q)\, dp^N\,dq^N$$

$\rho$ is the distribution function . It depends on the ensemble. Normalization:  

$$\int \rho(p,q) \, dp^N\,dq^N = 1$$ (5)

Question:

What is the distribution function for the microcanonical ensemble?

Answer:

It is zero if $E\ne E_0$, and satisfies (5). Therefore

$$\rho_{\text{microcanonical}} = \delta(E-E_0)$$