


Next: Entropy, Energy and Free
Up: Ensembles and Thermodynamic Potentials
Previous: Ensembles and Thermodynamic Potentials
- 1.
- For some system the dependence of the probability of micro-state
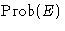 on energy was obtained for different temperatures:
on energy was obtained for different temperatures:
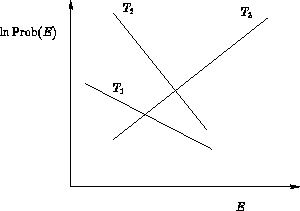
Check all statements that apply:
- (a)
- T1>T2>T3
- (b)
- T3>T2>T1
- (c)
- T2>T1
- (d)
- T3>0
- (e)
- T3<0
- Solution:
- Since
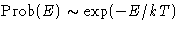 , the log of
probability depends on E linearly:
, the log of
probability depends on E linearly:
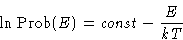
- If T>0 this is a decreasing function, so T1>0, T2>0,
T3<0
- The greater is T, the less steep is the line (what happens
if
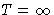 ?), so T1>T2>T3
?), so T1>T2>T3
- 2.
- Prove that
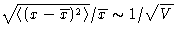 . What happens with fluctuations in the thermodynamic
limit?
. What happens with fluctuations in the thermodynamic
limit?
- Solution:
- A is an extensive value , X is an
intensive value. Therefore at
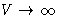 the scaling is
the scaling is 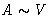 ,
, 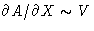 ,
, 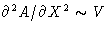 ,...
,...
We obtain:
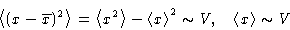
and
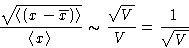
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Sep 9 22:39:08 EDT 1997
![]()
![]()
![]()
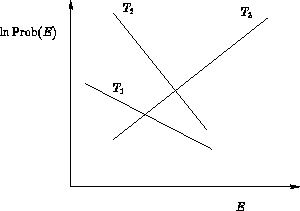
![]()
![]()
![]()