Subsections

• Averaging Entropy
• Aside: Legendre Transformations

Entropy, Energy and Free Energy in Canonical Ensemble

Averaging Entropy

We know how to calculate mean energy. How can we calculate mean entropy ?

Consider a macroscopic state with energy E in canonical ensemble:

Additivity of entropy:

S_A = S_M - S_B

Probability of a microscopic state in canonical ensemble: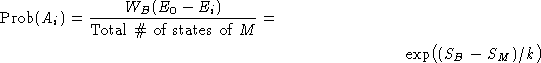
$$\begin{multline*} \Prob(A_i) = \frac{W_B(E_0-E_i)}{\text{Total \char93 of states of $M$}} =\ \exp\bigl((S_B-S_M)/k\bigr)\end{multline*}$$
We obtained:

$$S_A = -k\ln\bigl(\Prob(A_i)\bigr)$$

Entropy of a macroscopic state with energy E in a canonical ensemble equals minus k log of the distribution function

$$\Prob(A_i) = \frac{1}{Q}\exp(-E_i/kT)$$

Average entropy:
$$\begin{multline*} \left\langle S\right\rangle = -k\sum_E \Prob(E)\ln\bigl(\Prob(... ...{E_i}{kT}\right] = k\ln Q + \frac{\left\langle E\right\rangle}{T}\end{multline*}$$
Since $A=-kT\ln Q$, we obtained:

A = E - TS

We know that

$$dE = T\,dS - P\,dV$$

and since $d(TS)= T\,dS + S\,dT$,

$$dA = -S\,dT-P\,dV$$

Aside: Legendre Transformations

Suppose we have a function f(x). New variables:

$$p=f'(x), \quad p=p(x) \leftrightarrow x = x(p)$$

Consider the function

$$g(p) = f\bigl(x(p)\bigr) - px(p)$$

We see that:

$$dg = p\,dx - p\,dx - x\,dp = -x\,dp$$

or

g'(p) = -x

The function g is Legendre transformation of the function f.

Example: Hamilton & Lagrange Mechanics.

Free energy is Legendre transformation of energy (or entropy). In particular

$$\left(\frac{\partial E}{\partial S}\right)_V = T,\quad \left(\frac{\partial A}{\partial T}\right)_V = -S$$

It means that A=A(T,V)