Next: Quiz Up: Phase Equilibria Previous: Geometric Interpretation and Phase
![]()
![]()
![]()
Next: Quiz
Up: Phase Equilibria
Previous: Geometric Interpretation and Phase
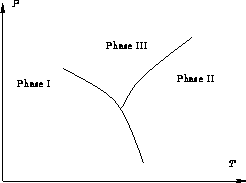
In each phase chemical potential ![]() is a function of P and
T. Phase equilibrium condition:
is a function of P and
T. Phase equilibrium condition:
![]()
![]()
Binary mixtures: we add a new variable--concentration c and have two
chemical potentials ![]() and
and ![]() . What is the largest number of
phases to coexist?
. What is the largest number of
phases to coexist?
If there are r phases, we have r+2 variables (P, T, cI, cII,...). There are 2r chemical potentials--2(r-1) equations. They have unique solution, if r+2=2(r-1), or r=4. In binary solutions four phases can coexist in a special point!
General case: n-component mixture, r phases. We have 2+r(n-1) variables for n(r-1) equations. Maximal value for r is 2+r(n-1)=n(r-1), or
r=n+2
This is Gibbs Phase Rule. The maximum number of phases in equilibrium is two plus the number of components.