Next: Gibbs Phase Rule Up: Phase Equilibria Previous: Free Energy Minima and
![]()
![]()
![]()
Next: Gibbs Phase Rule
Up: Phase Equilibria
Previous: Free Energy Minima and
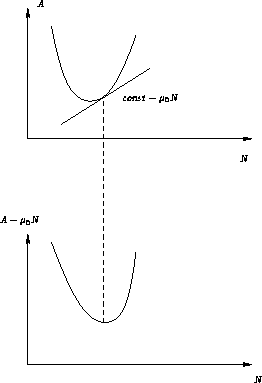
Suppose we have a system at constant ![]() . We minimize
. We minimize ![]() .
.
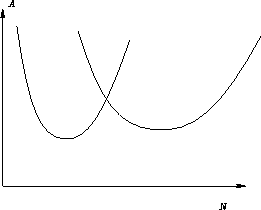
This means we make a line ![]() and the curve A(N). We want to
minimize the distance between the line and curve
and the curve A(N). We want to
minimize the distance between the line and curve ![]() we make
a tangent. If the curve is above tangent, the point is
locally stable, otherwise--unstable.
we make
a tangent. If the curve is above tangent, the point is
locally stable, otherwise--unstable.
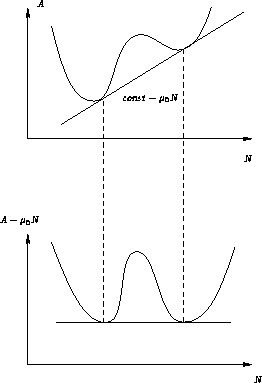
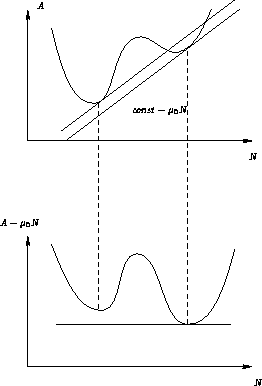
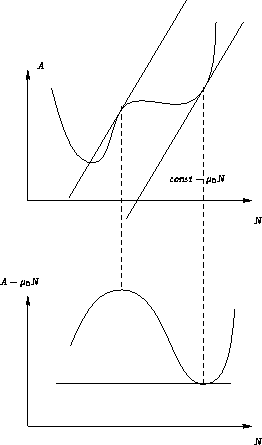
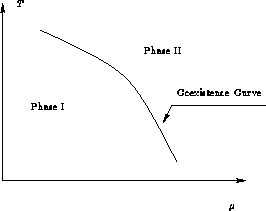
In ![]() -T space we have a coexistence curve:
-T space we have a coexistence curve:
In N-T space we have a coexistence region
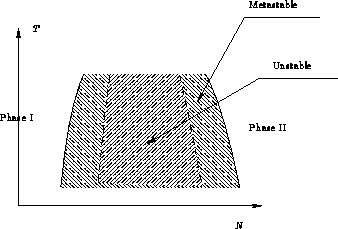
Why the difference? Because ![]() is intensive, and N is extensive
variable!
is intensive, and N is extensive
variable!
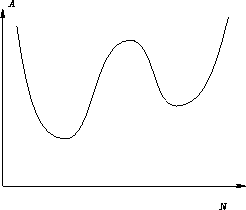
Is there an ending point for coexistence curve?
Two possibilities:
© 1997 Boris Veytsman and Michael Kotelyanskii