Next: Ising Model Up: Lattice simulations. Random Walk. Previous: Lattice simulations. Random Walk.
![]()
![]()
![]()
Next: Ising Model
Up: Lattice simulations. Random Walk.
Previous: Lattice simulations. Random Walk.
Following the spirit of the previous lecture, we start with the random walks. They are very important to study diffusion through the non-homogeneous media, and, of course, polymers. Here we will consider the simple example of the random walk on the square lattice in 2D. This can be a model for diffusion, or for non-self avoiding polymer chain.
We do a random walk, and now we are interested in its trajectory, as this simulates the polymer chain contour. And we are interested in the properties of this trajectory, as they describe the chain conformations, not just the probability density as a function of the coordinates. The important difference now is that we are building the chain, and we cannot stay at the same place, we must move at each step. But the direction where we move is decided by the MC procedure.
We consider an example of a polar chain with each bond having a dipole
moment ![]() of
of ![]() , parallel to the bond direction,
in the uniform electric field
, parallel to the bond direction,
in the uniform electric field ![]() . This model can actually describe
polymer chain in the flux, and liquid-crystalline ordering. The chain
is not self-avoiding, and all segments are independent. Each segment
contributes
. This model can actually describe
polymer chain in the flux, and liquid-crystalline ordering. The chain
is not self-avoiding, and all segments are independent. Each segment
contributes ![]() to the energy.
Probability distribution for conformation of a N-segment chain,
described by the set of bond vectors
to the energy.
Probability distribution for conformation of a N-segment chain,
described by the set of bond vectors ![]() is:
is:
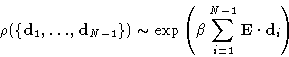
![]()
© 1997 Boris Veytsman and Michael Kotelyanskii