


Next: Periodic Boundaries for Off-Lattice
Up: Off-lattice Monte-Carlo Simulations. Lennard-Jones
Previous: Off-lattice Monte-Carlo Simulations. Lennard-Jones
The simplest off-lattice model of the liquid is a system of spherical
particles, interacting via a pairwise potential, that depends on the
distance between them, 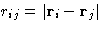 . As we know, molecules
repel, when they are very close to each other, but attract each other
at larger separation. The most widely used model for such interactions
is Lennard-Jones potential.
. As we know, molecules
repel, when they are very close to each other, but attract each other
at larger separation. The most widely used model for such interactions
is Lennard-Jones potential.
| 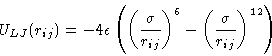 |
(1) |
Off-lattice Monte-Carlo Simulations.
Lennard-Jones Fluid
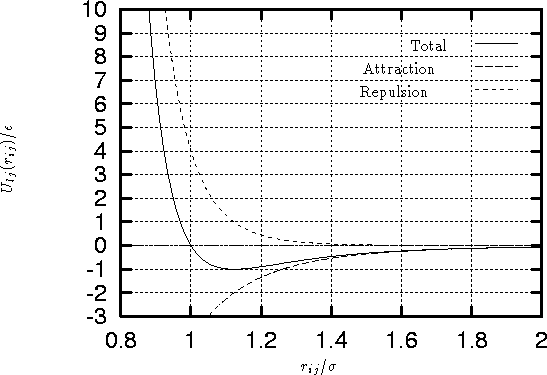
Figure 1:
Lennard-Jones 6-12 potential
 |
It is a sum of the short-range repulsive contribution 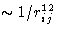 and attractive contribution
and attractive contribution 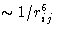 .
.
- Attractive term
- describes the interaction between two
molecules. When two atoms are brought close to each other, charge
density fluctuations in the first atoms's electron shell induce
polarization of the electron shell of the other. The attraction
between the two induced dipoles leads to the attractive inverse
sixth power term. Very similar interaction is observed between two
colloid particles, or polyelectrolyte molecules, where the induced
dipoles are due to the fluctuations of the counter-ion density
distribution. These fluctuations and the induced electron shell
polarization are described by very similar equations and therefore
lead to the similar answer. But their nature is very different.
The first one is due to the quantum fluctuations of the electron
shell interactions, the second is caused by the thermal fluctuations
of colloid particles, or polyions. Lennard-Jones
potential parameters should not depend on temperature, pressure,
etc.
The functional form (1/r6) comes from the exact
quantum-mechanical solution for the non-polar, neutral atoms with
the spherically symmetric electron shell, like e.g. noble gas
atoms.![[*]](/icons/foot_motif.gif) And therefore for
them it is exact. It is nevertheless always used as approximation
for other atoms.
And therefore for
them it is exact. It is nevertheless always used as approximation
for other atoms.
- Repulsive term
- Unlike attraction, the exact functional form for
the repulsive interaction is not well known and is approximated
either by the exponential, or by the inverse power term. Inverse
twelfth power is practical for the computer simulations, as it is
the square of 6, and hence the energy can be calculated faster.
- Parameters
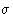 and
and 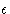
- As is seen from the
figure 1, and equation 1,
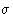 is a
measure of the atom's diameter, it's the distance where the energy
is zero. Minimum energy is at
is a
measure of the atom's diameter, it's the distance where the energy
is zero. Minimum energy is at 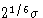 , and
, and 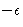 is
the minimal value of the energy. The values of this parameters are
usually extracted from some experimental data, like crystal
structures, thermodynamic properties, kinetic coefficients, etc.
They are very hard to get from the first principles.
is
the minimal value of the energy. The values of this parameters are
usually extracted from some experimental data, like crystal
structures, thermodynamic properties, kinetic coefficients, etc.
They are very hard to get from the first principles.



Next: Periodic Boundaries for Off-Lattice
Up: Off-lattice Monte-Carlo Simulations. Lennard-Jones
Previous: Off-lattice Monte-Carlo Simulations. Lennard-Jones
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Nov 11 18:36:02 EST 1997
![]()
![]()
![]()
![]() . As we know, molecules
repel, when they are very close to each other, but attract each other
at larger separation. The most widely used model for such interactions
is Lennard-Jones potential.
. As we know, molecules
repel, when they are very close to each other, but attract each other
at larger separation. The most widely used model for such interactions
is Lennard-Jones potential.
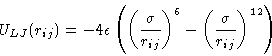
![]() and attractive contribution
and attractive contribution ![]() .
.
![]() And therefore for
them it is exact. It is nevertheless always used as approximation
for other atoms.
And therefore for
them it is exact. It is nevertheless always used as approximation
for other atoms.