Dynamic system. Equations of motion.

Dynamic system

is a system for which the following is defined:

• Coordinates and momenta (phase space)
• Kinetic and potential energies as functions of the coordinates and momenta

Example:

Two particles, interacting via the potential $v(\mathbf{r}_1,\mathbf{r}_2)$:

• Phase space: coordinates $(\mathbf{r}_1,\mathbf{r}_2)$, momenta $p_i=m_i\dot{\mathbf{r}_i},\ i=1,2$,
• Kinetic energy: $K=\displaystyle\sum_{i=1,2}\frac{p_i^2}{2m_i}$,
• Potential Energy: $\Pi=v(\mathbf{r}_1,\mathbf{r}_2)$

Newton Equations of motion:

 

$$m_i \ddot{\mathbf{r}_i} = \mathbf{F}_i = -\frac{\partial \Pi}{ \partial \mathbf{r}_i}$$ (1)

Hamiltonian. Hamilton equations:

Hamiltonian:  

$$\begin{aligned} H & = K + \Pi \ \dot{\mathbf{p}_i} & = -\f... ...athbf{r}_i} \ \dot{\mathbf{r}_i} & = \mathbf{p}_i\end{aligned}$$ (2)

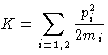When kinetic energy depends on momenta only, and not on coordinates, these two sets of equations are equivalent. This is always true if there is no constraints applied to the system, and the Cartesian coordinates are used. Here we will consider only such systems.

Molecular Dynamics (MD) simulation consists in numerical integration of the equations of motion. In its simplest form it reproduces the microcanonical ensemble, in which the energy is conserved.