Next: Lennard-Jones potential revisited Up: Molecular Dynamics I Previous: Dynamic system. Equations of
![]()
![]()
![]()
Next: Lennard-Jones potential revisited
Up: Molecular Dynamics I
Previous: Dynamic system. Equations of
If we have a system of N particles, then equations (1) represent a system of 3N second-order differential equations. It can be reduced to the system of 6N first-order differential equations by introducing additional variable for the first derivative of coordinate. This leads to (2).
Both of these systems can be solved numerically using a finite
difference technique. The general idea of the finite difference
method is the following: given the positions, velocities, and other
possible dynamic information at the time t, we attempt to obtain the
position, velocities, etc. at a later time ![]() with a
sufficient degree of accuracy. Trajectory (
with a
sufficient degree of accuracy. Trajectory (![]() etc.)
is obtained by the step-by-step evaluation of these quantities. The
choice of time step
etc.)
is obtained by the step-by-step evaluation of these quantities. The
choice of time step ![]() depends upon the numerical integration
method used and on the required accuracy. There exist many numerical
methods to solve the ordinary differential equations. Unfortunately,
not all of them satisfy the specific requirements of the molecular
dynamics simulations:
depends upon the numerical integration
method used and on the required accuracy. There exist many numerical
methods to solve the ordinary differential equations. Unfortunately,
not all of them satisfy the specific requirements of the molecular
dynamics simulations:
This algorithm, which exists in various versions, is the most popular
due to its simplicity and efficiency![]() .
.
Let's expand the coordinates at times ![]() and at
and at ![]() :
:
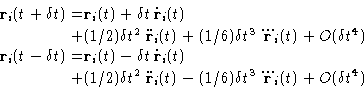 |
(3) |
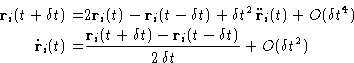 |
(4) |
Its main strength is that it allows to calculate coordinates with the
accuracy of ![]() , storing only three arrays: two
coordinates and accelerations, and calculating forces only once per
time step. This scheme is symmetric with respect to time
(
, storing only three arrays: two
coordinates and accelerations, and calculating forces only once per
time step. This scheme is symmetric with respect to time
(![]() and
and ![]() enter the
equations (4) symmetrically), and hence the algorithm is
time reversible. Velocities are not present explicitly in this
version. Although they can be calculated, but with a second order
accuracy. This is inconvenient, as this introduce some additional
``error'' in the energy or some other properties that depend on it.
Another potential drawback is that because the small, of the order of
enter the
equations (4) symmetrically), and hence the algorithm is
time reversible. Velocities are not present explicitly in this
version. Although they can be calculated, but with a second order
accuracy. This is inconvenient, as this introduce some additional
``error'' in the energy or some other properties that depend on it.
Another potential drawback is that because the small, of the order of
![]() , number is added to the difference in the
, number is added to the difference in the ![]() values, the rounding errors may be needlessly introduced.
Better estimate for the velocity can be obtained by the following
modification, also known as the ``velocity Verlet'' algorithm, which
stores the positions, velocities and accelerations at the same time
t:
values, the rounding errors may be needlessly introduced.
Better estimate for the velocity can be obtained by the following
modification, also known as the ``velocity Verlet'' algorithm, which
stores the positions, velocities and accelerations at the same time
t:
| |
(5) |
| |
(6) |
| |
(7) |
| |
(8) |
© 1997 Boris Veytsman and Michael Kotelyanskii