Next: Quiz Up: Molecular Dynamics at Constant Previous: Constant Temperature MD
![]()
![]()
![]()
Next: Quiz
Up: Molecular Dynamics at Constant
Previous: Constant Temperature MD
We have already seen in Monte
Carlo
, that isobaric simulations
should involve volume changes. So constant pressure MD naturally
involves the volume changes and its implementation requires the
equation of motion to describe its evolution. The technique described
below was proposed by Andersen in 1980, and involves coordinates
scaling, similar to NPT Monte Carlo, described previously.
![]()
First we introduce the constant pressure analog of the microcanonical ensemble--iso-enthalpic ensemble. We already know, how to make it work at a constant temperature. Now we will show how to make P constant.
Constant pressure is realized by the virtual ``piston'' of mass M
(which actually has units of ![]() ),
which is under constant force, that corresponds to the applied
pressure P0. Piston motion changes the volume of the system.
Additional kinetic
),
which is under constant force, that corresponds to the applied
pressure P0. Piston motion changes the volume of the system.
Additional kinetic ![]() and potential P0V energy terms,
coupled to the particles' momenta, are added to the Hamiltonian
(Hoover, 1985). The potential and kinetic energies of the particles
are written in terms of scaled variables
and potential P0V energy terms,
coupled to the particles' momenta, are added to the Hamiltonian
(Hoover, 1985). The potential and kinetic energies of the particles
are written in terms of scaled variables ![]() and
and ![]()
| (10) |
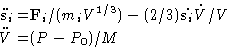 |
(11) |
Coupling this method to the Hoover thermostat by introducing another
variable ![]() (and
(and ![]() ), we can make the whole thing
reproduce the NPT ensemble. This can be again shown using Liouville
equation for the probability density distribution. NPT-MD
equations are:
), we can make the whole thing
reproduce the NPT ensemble. This can be again shown using Liouville
equation for the probability density distribution. NPT-MD
equations are:
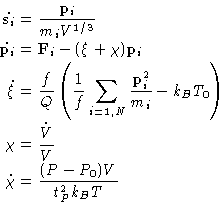 |
(12) |
Again a non-rigorous, but practical scheme, similar to the van Gunstern-Berendsen thermostat exists. It is called Berendsen barostat. It rescales the particle coordinates at every step by the factor
| (13) |
© 1997 Boris Veytsman and Michael Kotelyanskii