


Next: Interaction Energy
Up: Imperfect Gases and Liquids.
Previous: Imperfect Gases and Liquids.
- 1.
- Estimate the thermal speed of an oxygen molecule at room
temperature.
- Hint:
- There are NA molecules in
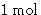
- Solution:
- Since
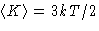 , average velocity is
, average velocity is
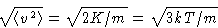
An average material scientist might not remember the mass of
oxygen molecule, but she/he certainly remembers its molar mass
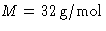 . Then m=M/NA. Recalling from Thermo
course that
. Then m=M/NA. Recalling from Thermo
course that 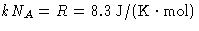 , we obtain:
, we obtain:
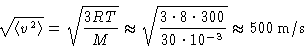
This is about 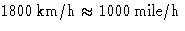
- 2.
- Calculate the chemical potential of ideal gas
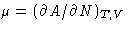 .
.
- Solution:
- Since
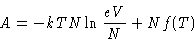
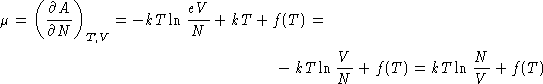
Chemical potential of ideal gas is kT log of the
concentration (up to a constant)!
- 3.
- Calculate the energy of the ideal gas without internal degrees
of freedom (
 ). If you are too lazy (or too smart) to
calculate it from equation
). If you are too lazy (or too smart) to
calculate it from equation
try to guess the answer. How would you do this?
- Solution:
- There are two ways to solve this problem.
- (a)
- Hard way. If
 ,
,
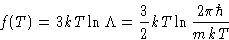
and
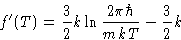
so
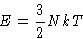
- (b)
- Smart way. If there are no internal degrees of freedom, all
the energy is kinetic energy K. This is 3kT/2 per particle,
or 3NkT/2 per N particles



Next: Interaction Energy
Up: Imperfect Gases and Liquids.
Previous: Imperfect Gases and Liquids.
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 18 22:50:29 EDT 1997
![]()
![]()
![]()
![]()
![]()
![]()
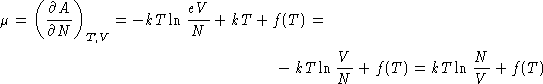
![]()
![]()
![]()