


Next: Virial Expansion
Up: Imperfect Gases and Liquids.
Previous: Quiz Answers
Subsections
We need to calculate configuration integral
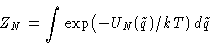
- 1.
- Analytic methods:
- (a)
- Exactly solvable problems (ideal gas, ideal crystal,
2D-lattice and others)
- (b)
- Expansions around solvable models: virial expansion, high- and
low-temperature expansions, imperfect solids...
- (c)
- Mean-field theories: neglecting fluctuations
- (d)
- Symmetry tricks--renormalization group etc.
- 2.
- Computer simulation (Monte Carlo)
In all cases we need U.
- Assumption:
- The total energy is the sum of pair interactions:
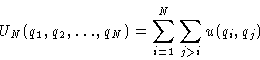
A good assumption for the majority of cases.
- Symmetry:
- For unstructured isotropic particles,
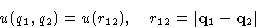
Let us discuss non-polar neutral monoatomic molecules. Let r
be the distance between them.
- 1.
- Molecules cannot come too close:
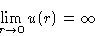
- 2.
- At large distances molecules do not interact
- 3.
- Molecules repeal each other at small distances and attract at
large distances.
- 4.
- Exact result: at
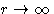 the energy is
the energy is
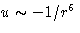 (dispersive forces)
(dispersive forces)
- ``Real Potential'':
-
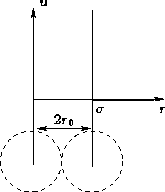
- Hard Core Potential:
- The simplest one
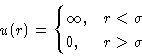
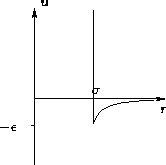
- Hard Core Plus Attraction:
- Slightly more complex
| 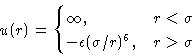 |
(2) |
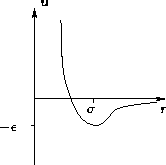
- Lennard-Jones Potential:
- The favorite among simulators
![\begin{displaymath}
u(r) = \epsilon\left[\left(\frac{\sigma}{r}\right)^{12} -
\left(\frac{\sigma}{r}\right)^{6}\right]
\end{displaymath}](img27.gif)
At 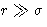 potential behaves as -1/r6--correct. At
potential behaves as -1/r6--correct. At
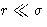 potential diverges
potential diverges 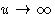 --correct.
--correct.
Why 12? Because computers calculate x2 very fast!
If you want to be realistic, you could add
- Complex interaction--Coulomb potential (very difficult!),
dipole-dipole interactions, multipole terms...
- Bonds: chemical, hydrogen,...
- ``Realistic'' potentials--QM Computations (Computer only!)



Next: Virial Expansion
Up: Imperfect Gases and Liquids.
Previous: Quiz Answers
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 18 22:50:29 EDT 1997
![]()
![]()
![]()
![]()
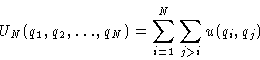
![]()
![]()
![]()

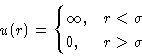

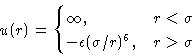

![]()