


Next: Distribution Functions
Up: Liquids. Density Correlation Functions
Previous: Liquids. Density Correlation Functions
- Problem of Virial Expansion:
- Virial expansion is a
polynomial in density
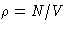 .
It is a continuous non-singular function of the density.
We know however, that the density cannot exceed the value of the closed
packing 0.74, therefore the equation of state should diverge.
Empirical recipe: let's cook some divergent function and fit it with
the known behavior at low densities.
.
It is a continuous non-singular function of the density.
We know however, that the density cannot exceed the value of the closed
packing 0.74, therefore the equation of state should diverge.
Empirical recipe: let's cook some divergent function and fit it with
the known behavior at low densities.
- Padé Approximants:
- Let us write
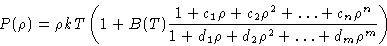
The expansion at small 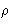 should coincide with virial expansion!
If we know N=n+m virial coefficients, (n,m)-Padé approximant
can be constructed. (3,3) approximant describes the simulation
(P,V,T) data for hard spheres a lot better, than the corresponding
virial expansion with 6 virial coefficients. This is however
empirical and ambiguous approach. Alternative description is
necessary.
should coincide with virial expansion!
If we know N=n+m virial coefficients, (n,m)-Padé approximant
can be constructed. (3,3) approximant describes the simulation
(P,V,T) data for hard spheres a lot better, than the corresponding
virial expansion with 6 virial coefficients. This is however
empirical and ambiguous approach. Alternative description is
necessary.
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 25 23:59:09 EDT 1997
![]()
![]()
![]()
![]()