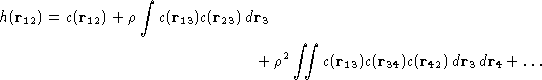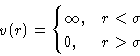Percus-Yevick Approximation
According to the Gibbs distribution, Probability, that n
particular particles of the N-particle system will be found at the
positions 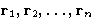 is:
is:
| 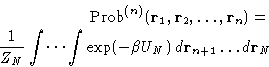 |
(1) |
The probability that any n particles are in the set of points:
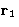 ,
, 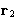 ,...,
,..., 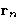 , irrespective
of the position of the rest N-n particles is:
, irrespective
of the position of the rest N-n particles is:

The factorials account for the number of ways to choose n particles
from N.
The simplest distribution function is the single particle
distribution function 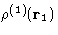 . This is just a probability
to find a molecule at the point
. This is just a probability
to find a molecule at the point 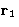 .
.
- Homogeneous fluid:
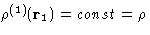 --the
overall density in the system.
--the
overall density in the system.
- Crystal:
- the periodic function
of the coordinates, corresponding to the crystal lattice.
- Inhomogeneous systems:
- confined liquids, or adsorbed
monolayers. It is not constant, and contains information about the
interface structure.
.
It is customary to define the n-particle correlation function
| 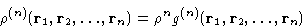 |
(2) |
If all particles are independent, 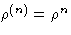 and
thus g(n) simply corrects for particle correlations.
and
thus g(n) simply corrects for particle correlations.
Obvious relationship between the correlation functions:
| 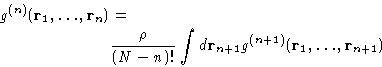 |
(3) |
For the reasons that we'll see below, the most important is the
pair correlation function 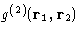 .In a homogeneous liquid of spherically symmetric molecules it depends only
on the distance
.In a homogeneous liquid of spherically symmetric molecules it depends only
on the distance 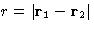 between two molecules.
For this reason it is also called the radial distribution function
between two molecules.
For this reason it is also called the radial distribution function
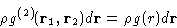
It is a ``probability'' to find a second molecule in 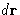 given that
there is a molecule at the origin of
given that
there is a molecule at the origin of 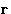 .
.
It is not normalized by 1 (see problem in the Quiz)
Due to the hard core repulsion of the molecules,
and as the molecules in liquid are uncorrelated at large distances.
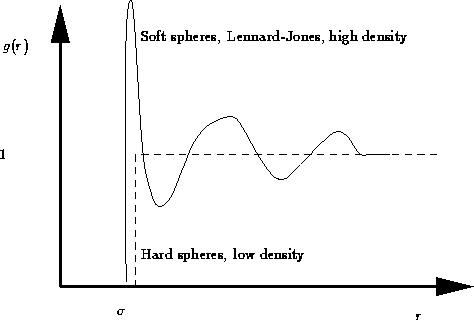
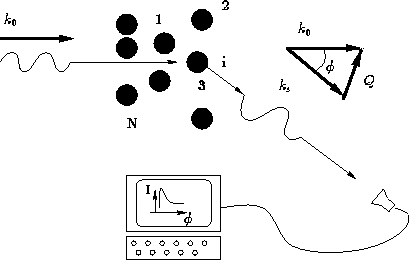
Consider the sample of gas, liquid, solid, glass, etc., containing N
molecules, irradiated by
X-rays, or neutrons, or light, or electrons, etc., with a wave
vector of 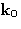 .We set detector to measure the radiation scattered at angle
.We set detector to measure the radiation scattered at angle 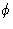 .
.
The intensity of the radiation scattered at angle 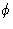 with the
wave vector
with the
wave vector 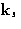 , and
, and 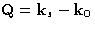 is
is
| 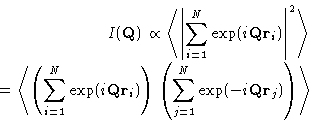 |
(4) |
We introduce microscopic density
| 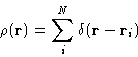 |
(5) |
It's Fourier transform can be defined as:
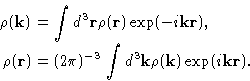
From (5) and (4)
| 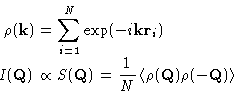 |
(6) |
The last equation defines the structure factor 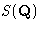 , which
is related to the density correlations and to the
, which
is related to the density correlations and to the 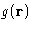 .
.
| 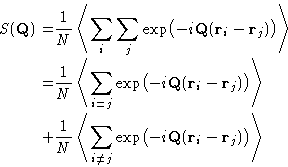 |
(7) |
The first term just equals 1. The second term is an average
of a sum over all pairs of molecules of a function 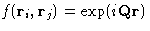 of their separation
of their separation 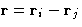 . As any
average, it can be rewritten as an integral of the
. As any
average, it can be rewritten as an integral of the
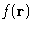 with the probability to observe
with the probability to observe 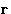 . It is
. It is
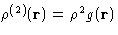 , given there is a molecule at the
origin.
, given there is a molecule at the
origin.
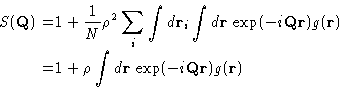
or just
| 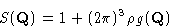 |
(8) |
with
| 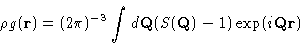 |
(9) |
- Note:
- In small angle scattering and fluctuation theory it is
customary to subtract the forward scattering in the definition of
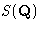 . Then
. Then
| 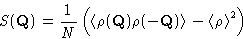 |
(10) |
- Energy:
- In the case of pairwise interactions, the average
potential energy is a sum over pairs:
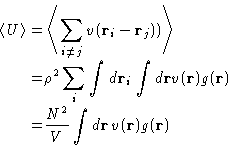
The total energy is then given as;
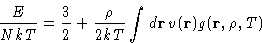
- Pressure:
-
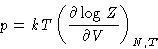
where
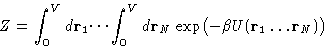
We can assume, that our liquid is in a cubic container and make the
coordinate change
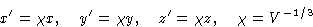
Then the distance between the particles:
rij=V1/3 rij'
and
| 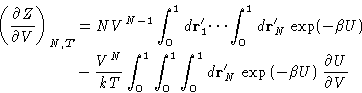 |
(11) |
with
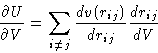
Now after going back to the initial coordinates and substituting the 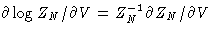 , and
again substituting the average of the sum over pairs by the integral
with g(r), as before, we finally obtain for the spherically
isotropic case:
, and
again substituting the average of the sum over pairs by the integral
with g(r), as before, we finally obtain for the spherically
isotropic case:
| 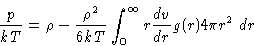 |
(12) |
This equation is called pressure equation. This is essentially
an equation of state in terms of the g(r).
- Virial Coefficients:
- If we expand:
| 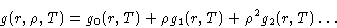 |
(13) |
and substitute it into (12) to get:
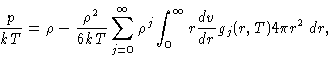
and compare the coefficients of the equal power of the density with the
virial expansion from the previous lecture, we obtain for the
virial coefficients:
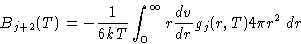
- Chemical Potential:
- So far we have established relationships of
the g(r) to the mechanical thermodynamic properties. To have a
complete description of the liquid we need a non-mechanical
thermodynamic function. (Why?) Let it be the chemical
potential. Let us assume that the system's energy is described by an
additional coupling parameter
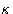 :
:
| 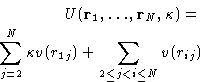 |
(14) |
This is equivalent to changing all interactions with the particle
number 1. All the other interactions remain unchanged. Changing
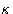 from to 1 switches between the system of particles
2,..., N, to the complete system of particles 1,..., N. We
will denote their configurational integrals as ZN-1 and ZN
respectively. By definition (with
from to 1 switches between the system of particles
2,..., N, to the complete system of particles 1,..., N. We
will denote their configurational integrals as ZN-1 and ZN
respectively. By definition (with 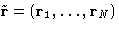 )
)
| 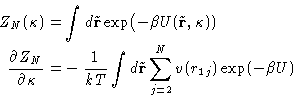 |
(15) |
Dividing by ZN, and again replacing the average of pair
contributions by the integral with 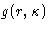 :
:
| 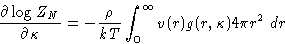 |
(16) |
Then
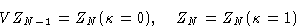
For very large N
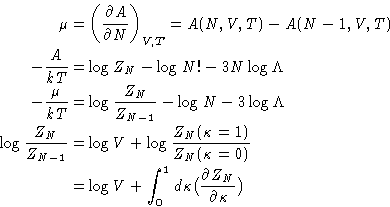
Putting this together with (16) gives finally:
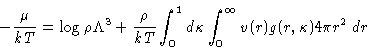
From 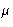 , p, and E, we can get any other thermodynamic
properties, if we knew
, p, and E, we can get any other thermodynamic
properties, if we knew 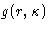
- Compressibility:
- We know that
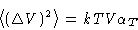
or, since 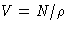 , we obtain for grand canonical ensemble
, we obtain for grand canonical ensemble 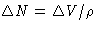 and
and
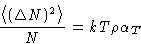
On the other hand![[*]](/icons/foot_motif.gif)
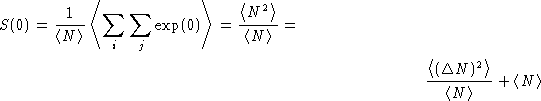
and
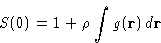
We obtained:
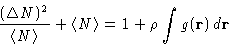
or, since
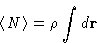
| 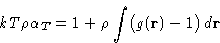 |
(17) |
This is called compressibility equation. If we know g(r),
we can obtain compressibility 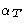
Describes the interaction between two
particles, immersed into the medium. Very important for description
of colloids, ions in solution, etc. Given that two particles are
separated by 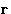 , what is their interaction?
, what is their interaction?
- Direct:
- via the intermolecular interaction potential
- Indirect:
- due to the presence of the other particles (medium)
This potential should, of course, be a function of
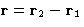 , and related to the probability for
, and related to the probability for 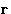 to occur,
or
to occur,
or 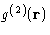 . Indeed it is defined as:
. Indeed it is defined as:
| 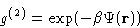 |
(18) |
It is easy to show (see the homework problem (5), that
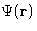 is in fact free energy of the whole system given
that particles 1 and 2 are
is in fact free energy of the whole system given
that particles 1 and 2 are 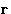 apart, and all the rest of the
system is averaged over. PMF is convenient to describe the
interaction of the various solutes (colloid particles, ions or
macromolecules in solution, etc.) It can also be used to describe the
``effective interaction'' of two molecules of the liquid, given their
relative position, and averaged over the possible configurations of
the rest.
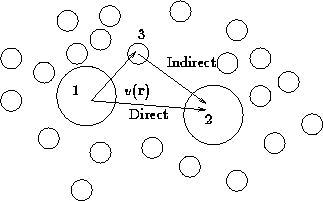
Consider triplet of particles: 1, 2, and 3:
The net force, acting on particle 1 is composed of
apart, and all the rest of the
system is averaged over. PMF is convenient to describe the
interaction of the various solutes (colloid particles, ions or
macromolecules in solution, etc.) It can also be used to describe the
``effective interaction'' of two molecules of the liquid, given their
relative position, and averaged over the possible configurations of
the rest.
Consider triplet of particles: 1, 2, and 3:
The net force, acting on particle 1 is composed of
- Direct interaction between 1 and 2,
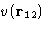 , and
, and
- Mean force due to 3, averaged over all it's positions with
the proper probability taking into account fixed positions of 1 and 2
| 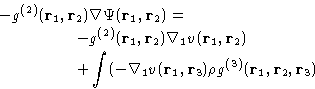 |
(19) |
This is the first equation of the BBGKY (Bogolyubov, Born, Green,
Kirkwood, Yvon) hierarchy. It relates the correlation functions of two
adjacent orders, and the inter-molecular interactions potential
v(r). Following the same line of argument we could derive similar
equations relating g(n), g(n+1), and v(r), for any n.
If we know the high-order correlation functions, we
could calculate, the lower- order ones, and then all the
thermodynamic properties. ![[*]](/icons/foot_motif.gif)
Still BBGKY is an infinite hierarchy of integral equations.
The simple way to close it at the second order is due to Kirkwood.
Assumption:
| 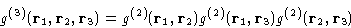 |
(20) |
This is called superposition approximation. (SPA) Using this
equation we can obtain the integral equation for g(2) and try to
solve it. Usually it can only be done numerically.
SPA assumes, that the correlations between any two molecules are
unaffected by the presence of the third one.
Equation (20) has been tested directly by computer simulations.
Although it is accurate only within 10% for hard spheres, it actually
describes the (P,V,T) properties quite well.
It also starts losing solutions at higher densities, which is believed to be
an offset of solidification.
Different closures, trying to capture three-body effects, and/or
considering higher-order correlations, have been considered in the
literature.
Instead of splitting the potential to direct an indirect, we can split
pair correlation function into direct and indirect
parts.
- Direct part:
- correlations due to interparticle interactions
between 1 and 2.
- Indirect part:
- Due to the presence of other particles.
- Ornstein-Zernike approach:
- At small
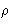 there are no
correlations:
there are no
correlations: 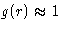 at
at 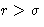 . We introduce
. We introduce
| 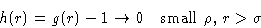 |
(21) |
Higher densities: 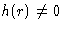 . We introduce c(r) describing
only binary collisions between 1 and 2 and
. We introduce c(r) describing
only binary collisions between 1 and 2 and
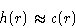
If potential is short-range, c(r) is also short range. At
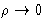 PMF tends to interparticle potential, and
PMF tends to interparticle potential, and
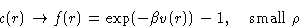
Even higher densities: both binary and ternary collisions:
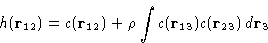
Then we add next terms...
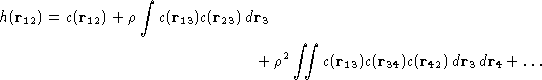
This could be represented as![[*]](/icons/foot_motif.gif) :
:
| 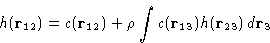 |
(22) |
This is an exact equation. It is a definition of direct
correlation function c(r).
- Model:
- Hard spheres.
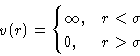
- Pair correlation function:
- inside spheres g(r)=0 at
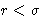
- Direct correlation function:
- small at
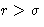 . Percus-Yevick assumption: c(r)=0 at
. Percus-Yevick assumption: c(r)=0 at 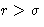
This allows analytical solution of equation (22) for
hard spheres. It gives us correlation function g(r) (c(r) and
h(r)).
From pressure equation of state (12)
| 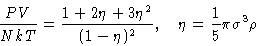 |
(23) |
From compressibility equation (17)
| 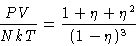 |
(24) |
- 1.
- Equations (23) and (24) give different
results! The theory is thermodynamically inconsistent.
- Reason:
- not any function g(r) gives thermodynamically consistent
theory--only the correct one. We made assumption for c(r)--and
must pay for it.
- Carhanan-Starling approximation:
- add equations (23)
and (24) with weights (1/3 and 2/3)
- Even better idea:
- adjust the weights.
- 2.
- Pressure diverges at
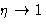 instead of
instead of 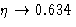 .
.



Next: Perturbation Theory
Up: Liquids. Density Correlation Functions
Previous: Problems of Liquids Theory
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 25 23:59:09 EDT 1997
![]()
![]()
![]()
![]() is:
is:
![]() ,
, ![]() ,...,
,..., ![]() , irrespective
of the position of the rest N-n particles is:
, irrespective
of the position of the rest N-n particles is:
![]()
![]() . This is just a probability
to find a molecule at the point
. This is just a probability
to find a molecule at the point ![]() .
.![]() and
thus g(n) simply corrects for particle correlations.
and
thus g(n) simply corrects for particle correlations.
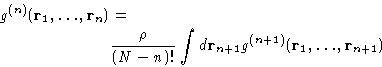
![]() .In a homogeneous liquid of spherically symmetric molecules it depends only
on the distance
.In a homogeneous liquid of spherically symmetric molecules it depends only
on the distance ![]() between two molecules.
For this reason it is also called the radial distribution function
between two molecules.
For this reason it is also called the radial distribution function
![]()
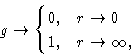


![]() .We set detector to measure the radiation scattered at angle
.We set detector to measure the radiation scattered at angle ![]() .
.![]() with the
wave vector
with the
wave vector ![]() , and
, and ![]() is
is
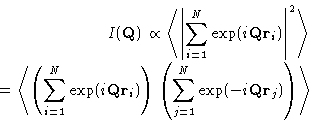
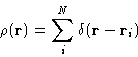
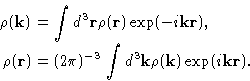
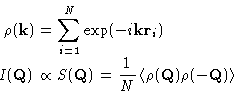
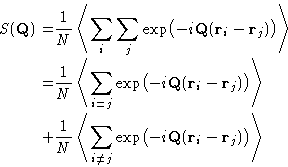
![]() of their separation
of their separation ![]() . As any
average, it can be rewritten as an integral of the
. As any
average, it can be rewritten as an integral of the
![]() with the probability to observe
with the probability to observe ![]() . It is
. It is
![]() , given there is a molecule at the
origin.
, given there is a molecule at the
origin.
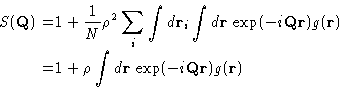
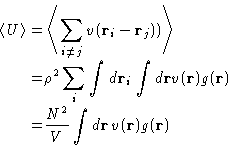
![]()
![]()
![]()
![]()
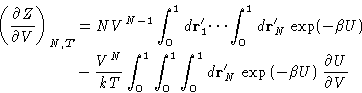
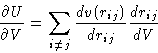
![]() , and
again substituting the average of the sum over pairs by the integral
with g(r), as before, we finally obtain for the spherically
isotropic case:
, and
again substituting the average of the sum over pairs by the integral
with g(r), as before, we finally obtain for the spherically
isotropic case:
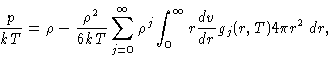
![]()
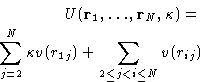
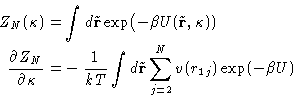
![]()
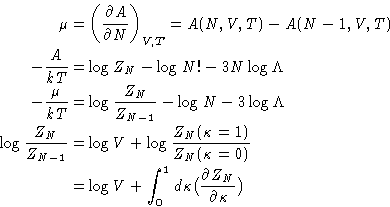
![]()
![]()
![]()
![]()
![]()
![]()
![]()

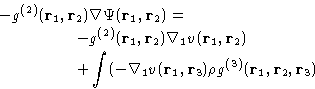
![]()
![]()
![]()