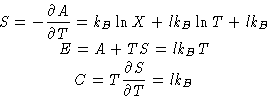Next: Harmonic Oscillator
Up: Solid State
Previous: Solid State
Subsections
Suppose we have l degrees of freedom (generalized
coordinates) q1, q2,..., ql and corresponding momenta
p1, p2,..., pl, and all q's are close to their
equilibrium values (take them to be zero, and qi will be deviations
from equilibrium positions): 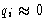 . We want to calculate
thermodynamics of such a system.
. We want to calculate
thermodynamics of such a system.
- Example:
- A simple model of a crystal--masses m on springs
with coefficients k. All masses sit near their equilibrium
positions! We have 3N degrees of freedom
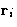 , i=1,..., N.
, i=1,..., N.
Kinetic energy:
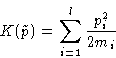
Potential energy: let's expand
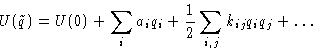
The first term does not matter--we'll drop it! The second term is
zero (we are at equilibrium!)
- Harmonic approximation:
- cubic and higher terms are small, and
| 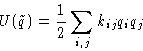 |
(1) |
This is quadratic form.
In harmonic approximation both potential and kinetic energy are
quadratic forms of coordinates and momenta.
- Example:
- For our crystal
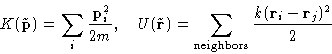
Expanding U, we recover quadratic form (1)
| 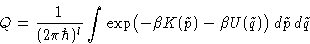 |
(2) |
with 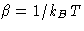
- Note:
- In this lecture we use partition function instead of
configuration integral and kB instead of k for Boltzmann
constant (why?)

New energy:
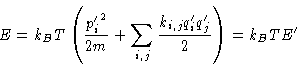
New differentials:
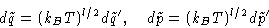
Classical partition function:
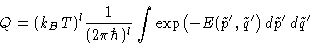
The integral does not depend on temperature!
Free energy:
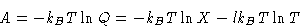
with X not dependent on T.
Entropy, energy and heat capacity:
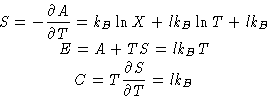
We have l degrees of freedom, and energy is lkBT: one kBT for
each degree of freedom!
What happens, if for some qi potential energy is zero (rotational
and translational degrees of freedom)? Then it contributes kBT/2.
In harmonic approximation for classical systems each degree of freedom
contributes kBT to energy and kB to heat capacity unless
potential energy is identically zero. In the latter case it
contributes kBT/2 and kB/2 correspondingly.
Examples:
- 1.
- Monoatomic ideal gas. 3N degrees of freedom. Energy
3kBTN/2, heat capacity 3kBN/2
- 2.
- Diatomic ideal gas, no vibrations. 5N degrees of freedom,
energy 5kBNT/2, heat capacity 5kBN/2
- 3.
- Diatomic ideal gas, vibration is allowed. 6N degrees of
freedom, one of them vibrational. Energy 7kBNT/2, heat capacity
7kBN/2
- 4.
- Solid body. 3N vibrational degrees of freedom. Energy
3kBNT, heat capacity 3kBN. Molar heat capacity 3R
(Dulong & Petit law).
Equipartition theorem is fine--except sometimes it does not work!
- 1.
- It predicts different results for gases whether we allow
vibration or not--but should not it be always allowed?
- 2.
- It predicts heat capacity 3kBN for solids. This is right--at high
temperatures. For diamond ``high'' means
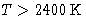 , sometimes it is 100-
, sometimes it is 100-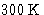 .
.
- Reason:
- Vibrations are not classical. They are quantum.
We need to include quantum mechanics to describe them properly!



Next: Harmonic Oscillator
Up: Solid State
Previous: Solid State
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Oct 1 00:45:35 EDT 1997
![]()
![]()
![]()
![]() . We want to calculate
thermodynamics of such a system.
. We want to calculate
thermodynamics of such a system.

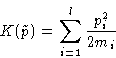
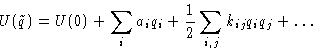
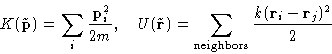
![]()
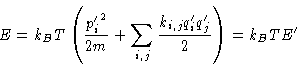
![]()
![]()
![]()