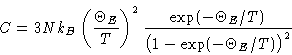Next: Debye Model of Crystals
Up: Solid State
Previous: Harmonic Oscillator
Assumptions:
- 1.
- Each atom has a certain equilibrium position in the lattice
- 2.
- Vibrations are harmonic with frequency
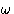
So we have 3N harmonic oscillators, and heat capacity
is
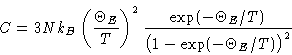
(Change NkB by R to obtain per mole value).
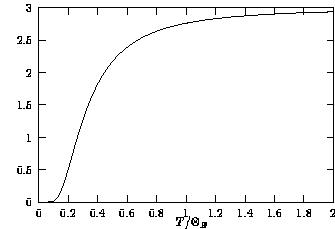
At 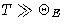 we recover classical behavior (C=3NkB). At low
T vibration is frozen:
we recover classical behavior (C=3NkB). At low
T vibration is frozen: 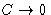 .
.
- Problem With Einstein Model:
- At low T heat capacity is
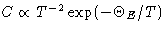 . This
is too fast! The experimental result is
. This
is too fast! The experimental result is 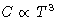 .
. - Reason:
- Atoms move cooperatively: if atom A goes to the left, its
neighbor might accommodate by going the same way! Einstein model does
not account for this.
We must introduce collective motion.
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Oct 1 00:45:35 EDT 1997
![]()
![]()
![]()