


Next: Quiz
Up: Solid State
Previous: Einstein Model of Crystals
Subsections
We![[*]](/icons/foot_motif.gif) represented each atom as a
harmonic oscillator. It did not work.
represented each atom as a
harmonic oscillator. It did not work.
Let us represent our system as a set of 3N oscillators, but choose
them differently, including collective motion.
We have N particles with masses m on springs k:
Equation of motion:
| 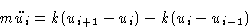 |
(3) |
or
| 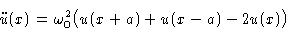 |
(4) |
Periodic boundary conditions: u1=uN+1. Sound velocity:
| 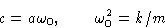 |
(5) |
All ui are entangled! To disentangle them--use a
trick![[*]](/icons/foot_motif.gif) :
:
| 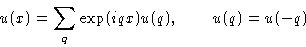 |
(6) |
What can we say about q? We want u(Na)=u(0), or
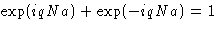 for all q. This means that
for all q. This means that 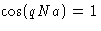 ,or
,or
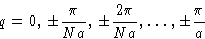
Physics: we represented deviation as sum of waves:
These waves are called modes
Substitute (6) into (4):
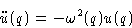
with
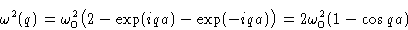
For small q
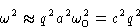
Solution:
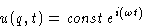
In real space we obtain sum of terms proportional to
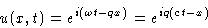
This describes sound waves propagating with velocity c (that
is why we claimed that c is sound velocity)
Equation
| 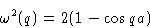 |
(7) |
is called dispersion equation. Each q corresponds to one
normal mode or one kind of phonons--in other words, to a sound
wave.
Why Debye model is better than Einstein model: since 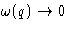 at
at 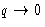 , some phonons are excited even at low temperatures!
, some phonons are excited even at low temperatures!
We obtained N independent oscillators (modes!) with frequencies
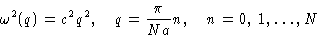
Each gives a contribution  to the heat
capacity. Total contribution:
to the heat
capacity. Total contribution:
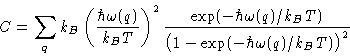
If 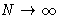 --integration instead of summation. We have N values
for q in the interval
--integration instead of summation. We have N values
for q in the interval ![$[0,\pi/a]$](img66.gif) --so
--so
What's new for 3D?
- 1.
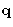 is now vector--instead of dq we must integrate
over
is now vector--instead of dq we must integrate
over 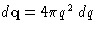 , q2=qx2+qy2+qz2.
, q2=qx2+qy2+qz2.
- 2.
- There are three waves for every
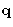 : two transversal and one
longitudinal
: two transversal and one
longitudinal
Instead of integrating by 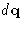 we integrate by
we integrate by 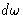 . Number of
modes:
. Number of
modes:
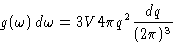
Limits:
lower limit 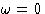 , upper limit should be
, upper limit should be 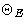 , but
we used
, but
we used 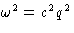 instead of exact
equation (7), so we correct this by taking
instead of exact
equation (7), so we correct this by taking 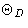 instead:
instead:
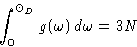
Result (for simple lattice!):
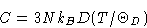
with
| 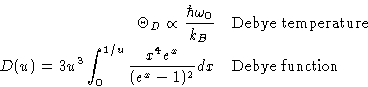 |
(8) |
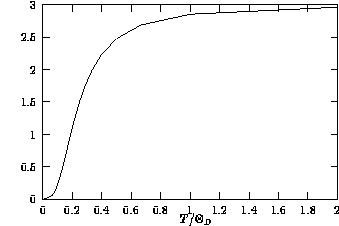
- High temperatures:
- for
 upper limit in the integral
in (8) is small (1/u),
upper limit in the integral
in (8) is small (1/u),
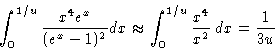
and C=3NkB
- Low temperatures:
- for
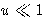 integral is constant, and
integral is constant, and 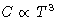
. This is an example of a scaling, made by a classic
of physics as early as 1912!



Next: Quiz
Up: Solid State
Previous: Einstein Model of Crystals
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Oct 1 00:45:35 EDT 1997
![]()
![]()
![]()
![]() represented each atom as a
harmonic oscillator. It did not work.
represented each atom as a
harmonic oscillator. It did not work.
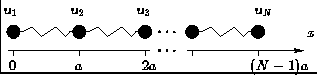
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]() at
at ![]() , some phonons are excited even at low temperatures!
, some phonons are excited even at low temperatures!
![]()
![]() to the heat
capacity. Total contribution:
to the heat
capacity. Total contribution:
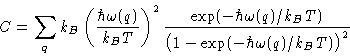
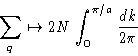
![]() we integrate by
we integrate by ![]() . Number of
modes:
. Number of
modes:
![]()
![]()
![]()
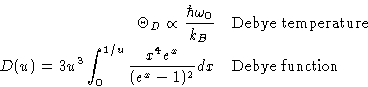
![]()