Next: Inhomogeneous Systems Up: Fluctuations in Inhomogeneous Systems. Previous: Fluctuations in Inhomogeneous Systems.
![]()
![]()
![]()
Next: Inhomogeneous Systems
Up: Fluctuations in Inhomogeneous Systems.
Previous: Fluctuations in Inhomogeneous Systems.
We already know the theory of fluctuations of one variable . Just a reminder...
Professor: Do you know this?Students: No.
Professor: Did you know this last semester?
Students: No.
Professor: Were you taught this last semester?
Students: Yes.
Illustration to the Method of Successive Iterations
Suppose we have one variable x. Near equilibrium we construct the
thermodynamic potential A(x) for a subsystem: the free energy
of the subsystem at given x. The total free energy of the subsystem
plus the environment is minimal:
![]() . We use Lagrange multiplier and
obtain
. We use Lagrange multiplier and
obtain
![]()
Probability of a fluctuation is determined by the entropy of the whole system:
![]()
| |
(1) |
![]()
![]()
We obtained:
![]()
![]()
![]()
![]()
Averages are:
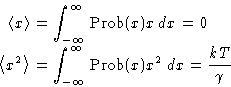
Free energy:
![]()
![]()
| |
(2) |
Suppose we have many variables xi, i=1, 2,..., n. Let the equilibrium value
![]()
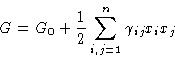 |
(3) |
Let
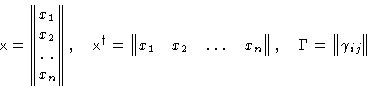
![]()
Let us make a linear transformation:
xi = tik yk
Then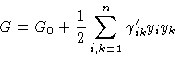
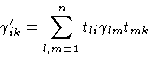
![]()
![]()
Mathematicians prove, that symmetric matrix ![]() can be
diagonalized: there exists matrix
can be
diagonalized: there exists matrix ![]() such as
such as
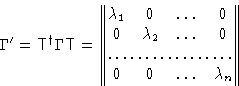
The quadratic form (3) becomes
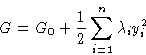
![]()
Let us calculate ![]() :
:
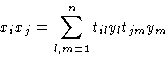
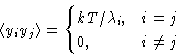
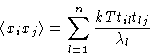
© 1997 Boris Veytsman and Michael Kotelyanskii