


Next: Universality and Scaling Invariance
Up: Fluctuations in Inhomogeneous Systems.
Previous: Fluctuations in Homogeneous Systems
Subsections
In inhomogeneous systems G depends on the value of x in all
points 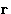 . G is a functional
. G is a functional 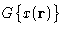 --it
depends on a function
--it
depends on a function 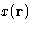 .
.
- Analogy with multi variable case:
- we have variables
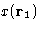 ,
,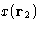 ,..., and want to minimize G.
,..., and want to minimize G.
- Idea:
- Introduce normal coordinates that diagonalize G
- Trick:
- Use Fourier transform--it leads to normal coordinates
in linear problems
For inhomogeneous system the free energy is
![\begin{displaymath}
G= G_0 + \int\left[aM^2+dM^4-HM+g\left(\nabla
M\right)^2\right]\,d\mathbf{r}\end{displaymath}](img43.gif)
Assumptions and simplifications:
- 1.
- We are above critical point, so a>0 (for negative a we
expand around M0)
- 2.
- We neglect the term dM4, This is the most important
approximation!!!
Then we make Fourier transform:
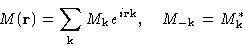
Quadratic term:
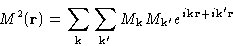
Gradient term:
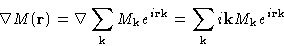
and
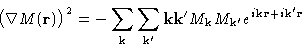
Term with external field:
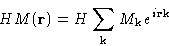
Mathematical result
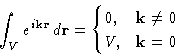
Integrals with quadratic & gradient terms contain
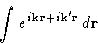
This is non-zero only if 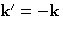 . Then
. Then
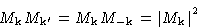
and we obtain
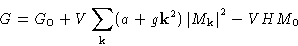
We represented free energy as a sum over Fourier components--this
means 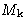 are normal coordinates!
are normal coordinates!
We immediately obtain for fluctuations
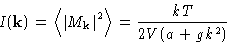
This is exactly the function measured in scattering experiments!
What happens near critical points? Here 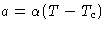 is small.
is small.
- 1.
- Short wavelength fluctuations do not depend on the temperature:
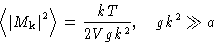
- 2.
- Long wavelength fluctuations grow:
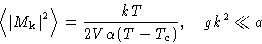
- 3.
- The characteristic wavelength tends to infinity:
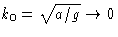
This is called critical opalescence
The function
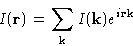
Is called correlation function. It is just![[*]](/icons/foot_motif.gif)
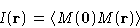
Integrating 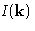 , we obtain:
, we obtain:
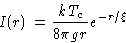
with correlation radius
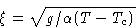
This function is called Ornstein-Zernicke function.
What happens at 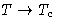 ? Correlation radius
? Correlation radius 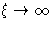
- 1.
- At
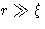 we have exponential decay with distance
we have exponential decay with distance
- 2.
- At
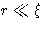 correlations decay as 1/r and are independent of
the temperature!
correlations decay as 1/r and are independent of
the temperature!
Above we obtained the formula
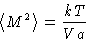
This works in thermodynamic limit 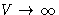 . In other words
. In other words
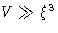 . Near Tc this condition becomes very stringent!
. Near Tc this condition becomes very stringent!
Landau theory works if fluctuations are small. Average fluctuation in
the volume 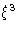 is
is
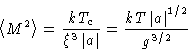
Comparing this to the equilibrium value below critical point
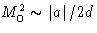 , we obtain that
, we obtain that 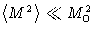 if
if
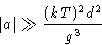
or, since 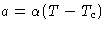
| 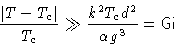 |
(4) |
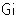 is Ginsburg number.
is Ginsburg number.
Landau theory works, if we are both:
- 1.
- Close to critical point, so
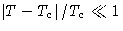 (we used
expansion!)
(we used
expansion!)
- 2.
- Still not close enough, so
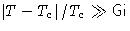 .
.
Why does Landau theory work well for polymers? Coefficient g does not
depend on molecular weight N, but 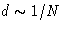 and
and 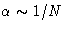 . We
obtain
. We
obtain 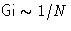 , i.e. Ginsburg number is small.
, i.e. Ginsburg number is small.



Next: Universality and Scaling Invariance
Up: Fluctuations in Inhomogeneous Systems.
Previous: Fluctuations in Homogeneous Systems
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 28 22:10:23 EST 1997
![]()
![]()
![]()
![]() . G is a functional
. G is a functional ![]() --it
depends on a function
--it
depends on a function ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
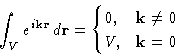
![]()
![]()
![]()
![]()
![]() is small.
is small.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ? Correlation radius
? Correlation radius ![]()
![]()
![]() is
is
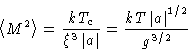
![]()
![]() and
and ![]() . We
obtain
. We
obtain ![]() , i.e. Ginsburg number is small.
, i.e. Ginsburg number is small.