


Up: Fluctuations in Inhomogeneous Systems.
Previous: Inhomogeneous Systems
Subsections
We neglected the term dM4. If we include it, free energy is no
longer a sum of independent terms--fluctuations interact!
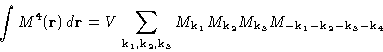
When fluctuations are small, we can expand this term. When they are
not--we are out of luck!
Close enough to critical point only interactions of long wavelength
fluctuations determine the properties. But the long wavelength limit
is described by Landau Hamiltonian!
In other words, near critical point we start from Landau expression,
calculate fluctuations and their interactions--and obtain everything!
- Universality:
- Close enough to critical point
(
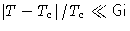 ) the behavior of the system is determined
only by the symmetry of order parameter.
) the behavior of the system is determined
only by the symmetry of order parameter.
In particular, for scalar order parameter all systems can be
described by partition function
| ![\begin{displaymath}
\Xi = \int\mathcal{D}M(\mathbf{r})\,\exp\left[-\beta\int
(aM^2+dM^4-HM)\,d\mathbf{r}\right]
\end{displaymath}](img86.gif) |
(5) |
where 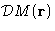 is integral over all realizations of
is integral over all realizations of
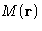 .
.
Now we need to calculate (5)--a very tough task!
Fluctuations with the wavelength 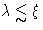 do not ``feel'' the
critical point. The only fluctuations that do, are those with
do not ``feel'' the
critical point. The only fluctuations that do, are those with
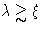
- Scaling Hypothesis:
- The fluctuations at all length scales look
exactly the same. Change of the length scale can be
compensated by the change of the temperature
- Renormalization Group Approach:
- We change length scale
in (5) and require
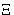 to be invariant! By this method
people obtained approximation for
to be invariant! By this method
people obtained approximation for 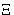 (and received Nobel Prize).
(and received Nobel Prize).



Up: Fluctuations in Inhomogeneous Systems.
Previous: Inhomogeneous Systems
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 28 22:10:23 EST 1997
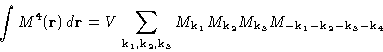
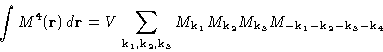
![]() do not ``feel'' the
critical point. The only fluctuations that do, are those with
do not ``feel'' the
critical point. The only fluctuations that do, are those with
![]()