Next: Thermodynamic Forces & Kinetic Up: Time Dependent Fluctuations Previous: Time Dependent Fluctuations
![]()
![]()
![]()
Next: Thermodynamic Forces & Kinetic
Up: Time Dependent Fluctuations
Previous: Time Dependent Fluctuations
Suppose we have a thermodynamic variable x with ![]() . What
happens if at some moment
. What
happens if at some moment ![]() ?
?
| |
(1) |
At ![]() we have
we have ![]() (why?). For
small deviations
(why?). For
small deviations ![]() is small. We can expand it in
series in
is small. We can expand it in
series in ![]() , and
, and
| |
(2) |
| |
(3) |
This formula is valid only for t>0: we can prepare an ensemble with given x0 and observe it, but cannot go backward! This is another manifestation of time irreversibility.
For space-dependent problems we defined the correlation
function ![]() . For time-dependent case we define
time correlation function
. For time-dependent case we define
time correlation function ![]() . We want
to calculate
. We want
to calculate ![]() . This is the averaging over the ensemble of
systems with arbitrary x(0). Note this difference with the previous
case: there we had x(0) fixed, and used restricted ensembles.
Now we return to the general case and consider equilibrium
ensemble.
. This is the averaging over the ensemble of
systems with arbitrary x(0). Note this difference with the previous
case: there we had x(0) fixed, and used restricted ensembles.
Now we return to the general case and consider equilibrium
ensemble.
Translation along the time axis:
![]()
| |
(4) |
Double averaging method:
![]()
![]()
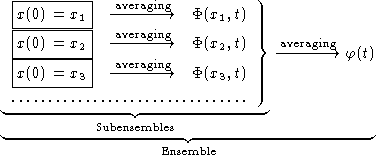
Since in a subensemble x(0) is given,
![]()
![]()
We obtained for the correlation function:
![]()
| |
(5) |
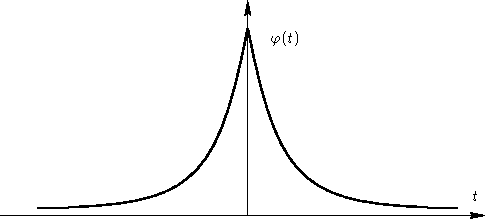
We have several variables xi. Kinetic equations:
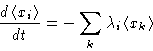
![]()
![]()
| |
(6) |
| |
(7) |
| |
(8) |
© 1997 Boris Veytsman and Michael Kotelyanskii