


Up: Time Dependent Fluctuations
Previous: Relaxation & Time Correlation
Subsections
- Thermodynamic force:
- We introduced before conjugated variables:
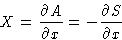
Let us set zero at the equilibrium value: 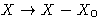 . This is called thermodynamic force.
. This is called thermodynamic force.
- Examples:
- If x is volume, the force is X=-(P-P0), if x
is the number of particles,
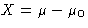 , etc.
, etc.
In equilibrium (x=0) we have:
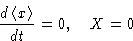
When x>0, 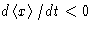 and X>0:
and X>0:
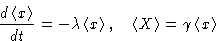
From these equations
| 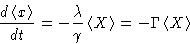 |
(9) |
The new variable 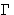 is called kinetic (or Onsager)
coefficient. We have
is called kinetic (or Onsager)
coefficient. We have 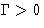 (why?).
(why?).
Two ways to create a fluctuation:
- 1.
- Apply an external force X
- 2.
- Wait long enough, and it will happen
![[*]](/icons/foot_motif.gif)
Equation (9) shows that these two ways are
equivalent. No matter how we created a fluctuation, it will relax in
the same way.
Suppose we have many variables xi. We have many
thermodynamic forces Xi. Equations for relaxation:
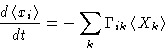
- Onsager Law:
- The coefficients are symmetric:
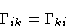
This equation can be proved from the symmetry with respect to time
inversion: 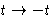 .
.



Up: Time Dependent Fluctuations
Previous: Relaxation & Time Correlation
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 28 22:13:33 EST 1997
![]()
![]()
![]()
![]()
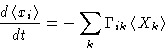
![]()