Next: Canonical Ensemble Up: Probabilities of Macroscopic States. Previous: Probabilities of Macroscopic States.
![]()
![]()
![]()
Next: Canonical Ensemble
Up: Probabilities of Macroscopic States.
Previous: Probabilities of Macroscopic States.
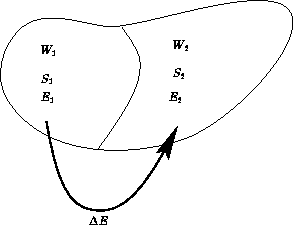
Two macroscopic states A and B. Suppose S(A)>S(B). What can we say about probabilities?
All microscopic states in microcanonical ensemble are equal. Probability is proportional to the number of states.
![]()
Thermodynamic limit: ![]() ,
, ![]() ,
, ![]()
![]()
Equations of mechanics are time reversible . How can irreversibility appear in the picture?
Glass falls from a table an is broken. All molecular motions are reversible. What about irreversibility??
Happy families are all alike; every unhappy family is unhappy in its own way.
![]()
![]()
![]()
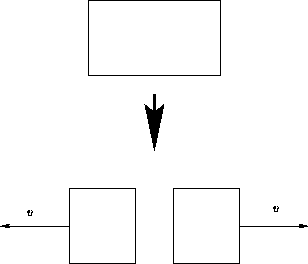
We discussed systems that do not move. What happens if it moves with the velocity v?
Entropy depends only on the internal energy:
![]()
![]()
In fully equilibrated systems T>0. But partially equilibrated systems might have negative T for some degrees of freedom.
© 1997 Boris Veytsman and Michael Kotelyanskii