


Next: Statistical Mechanics and Thermodynamics
Up: Probabilities of Macroscopic States.
Previous: Entropy and Probabilities
Subsections
Let us take a part of Microcanonical Ensemble M. This part is
described by canonical ensemble , if the size of the rest
(thermal bath ) tends to infinity.

What is the probability for A to be in the
microscopical state i with energy EA=Ei?
- All states in the microcanonical ensemble with the same
energy E0 are equally probable. If Ai is fixed, only B can
change
|  |
(1) |
- Total energy:
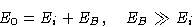
- Probability for Ai
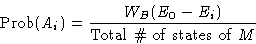
We want to use thermodynamic limit: 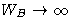 ,
, 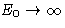 . We
hope that the answer does not depend on the nature of the
thermal bath.
. We
hope that the answer does not depend on the nature of the
thermal bath.
- Naïve approach:
- Let us expand WB:
- Why it does not work:
- Taylor expansion works only if the
next term is smaller than the previous.
We need
|  |
(2) |
But SB and E0 are extensive variables. The derivative is
intensive and does not blow up. We are not
guaranteed that (2) works!![[*]](/icons/foot_motif.gif)
- A better way:
- Let us expand SB(E) instead:
Thermodynamic limit (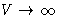 )
)
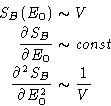
Large term SB(E0) is canceled by denominator in (1). We
are left with the second term.
- Answer:
- For the canonical ensemble
| 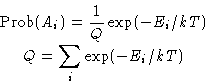 |
(3) |
This is Gibbs formula .
In microcanonical ensemble all states are equal. In canonical ensemble
states with lower energy are more equal than others![[*]](/icons/foot_motif.gif) !
!
Dependence on the thermal bath: only through T. All thermal baths
with the same T are equivalent.
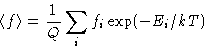
Particular case:
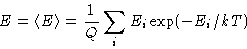



Next: Statistical Mechanics and Thermodynamics
Up: Probabilities of Macroscopic States.
Previous: Entropy and Probabilities
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 4 21:28:23 EDT 1997
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
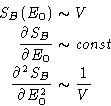
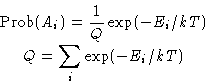
![]()
![]()