Subsections

• Definitions
• Derivatives

Partition Function and Free Energy

Put off thy shoes from off thy feet, for the place whereon thou standest is holy ground.

Exodus, 3:5

Definitions

The normalization constant in the canonical ensemble

$$Q = \sum_i \exp(-E_i/kT)$$

is called partition function . The quantity

$$A = -kT\ln Q$$

is called free energy .

Derivatives

Let us calculate $(\partial (A/T)/\partial (1/T))_V$:
$$\begin{multline*} \frac{\partial (A/T)}{\partial (1/T)} = -\frac{\partial k\ln Q... ...frac{1}{Q} \sum_i E_i \exp(-E_i/kT) = \left\langle E\right\rangle\end{multline*}$$

$$\frac{\partial (A/T)}{\partial (1/T)} = E\quad\text{or} E = -kT^2 \left(\frac{\partial (A/T)}{\partial T}\right)_V$$

If we know partition function, we can calculate average energy!

Conjugated Fields:

Variable X is a conjugated field to x_i, if

$$\frac{\partial E_i}{\partial X} = -x_i$$

If one is extensive, another is intensive!

Examples:

pressure (x) & volume (X), magnetization (x) & field (X),...

Let us calculate derivative:
$$\begin{multline*} \frac{\partial A}{\partial X} = -kT \frac{\partial \ln Q}{\par... ...{1}{Q} \sum_i x_i\exp(-E_i/kT) = - \left\langle x \right\rangle \end{multline*}$$
If we know partition function, we can calculate averages!

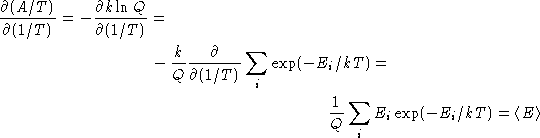
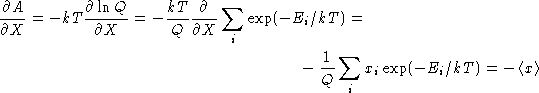
Second derivative:
$$\begin{multline*} \frac{\partial^2 A}{\partial X^2} = \\ \frac{1}{Q^2}\frac{\pa... ... \left\langle x \right\rangle^2 - \left\langle x^2 \right\rangle\end{multline*}$$
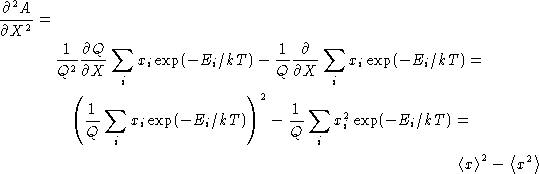
This is mean squared fluctuation!

We obtained  

$$\frac{\partial A}{\partial X} = - \left\langle x \right\ran... ...eft\langle x \right\rangle^2 - \left\langle x^2 \right\rangle$$ (5)

We can obtain all information about our system from differentiating free energy!