Subsections

• Pressure
• Heat and Entropy

Statistical Mechanics and Thermodynamics

Pressure

Let us change the volume reversible . Then 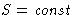$S=\mathit{const}$. We define pressure as

$$P = -\left(\frac{\partial E}{\partial V}\right)_S$$

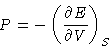
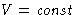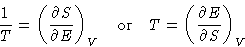
In the definition of temperature we implicitly held $V=\mathit{const}$:

$$\frac1T = \left(\frac{\partial S}{\partial E}\right)_V \quad\text{or}\quad T = \left(\frac{\partial E}{\partial S}\right)_V$$

Therefore  

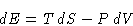$$dE = T\,dS - P\,dV$$ (4)

Heat and Entropy

What do we know about heat from Thermodynamics?

1.

There is ``entropy'' S'. In closed systems 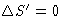$\Delta S'=0$ for reversible processes and 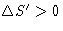$\Delta S'\gt$ for irreversible processes (Second Law)

2.

Energy is conserved: for reversible processes in open systems 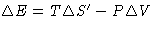$\Delta E = T\Delta S' - P\Delta V$ (First Law)

What did we found about our entropy 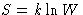$S=k\ln W$? Exactly same things!

Conjecture:

These things are same: S=S'.

Meaning of the Boltzmann Constant:

If we defined entropy as 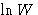$\ln W$, temperature would have dimension of energy. We measure temperature differently--and must pay for it by adding a constant!

We can prove all postulates of thermodynamics from statistics!