


Next: Homework Problems
Up: Ensembles and Thermodynamic Potentials
Previous: General Case: How to
Subsections
Compare the partition function and grand partition function:
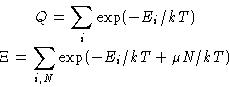
we see that
| 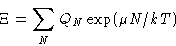 |
(2) |
We can express one partition function through other!
Two connections between canonical and grand canonical ensembles:
- 1.
- A system in canonical ensemble can be divided into parts.
Each part can be considered in grand canonical ensemble with
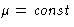 !
!
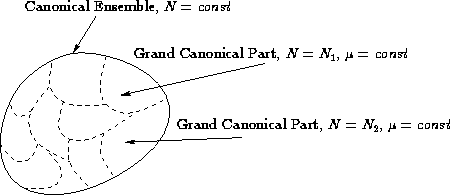
- 2.
- A system in grand canonical ensemble can be considered as
a set of systems, each of them in canonical ensemble with
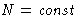
These two ways reflect a deep connection between the function and its
Legendre Transform.
Through this method we can connect any two ensembles!
In our calculations we often substituted 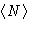 for
N. But in canonical ensembles
for
N. But in canonical ensembles 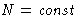 , in grand canonical
ensemble
, in grand canonical
ensemble 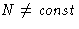 . Did we cheat?
. Did we cheat?
- Theorem:
- suppose we have a sum
| 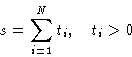 |
(3) |
and
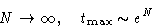
Then at 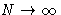
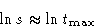
- Proof:
- For any N
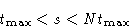
Take log:
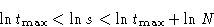
At 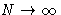 we have
we have 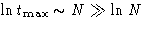 , and the
theorem is proven.
, and the
theorem is proven.
- Consequence:
- In the sum (2) all terms are
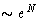 . In the thermodynamic limit
. In the thermodynamic limit
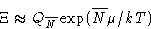
with such N that
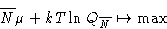
or
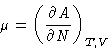
Your teachers did not cheat you--at least in the thermodynamic
limit!



Next: Homework Problems
Up: Ensembles and Thermodynamic Potentials
Previous: General Case: How to
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Sep 9 22:39:08 EDT 1997
![]()
![]()
![]()
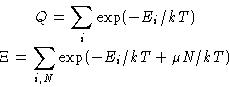

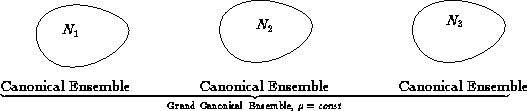
![]() for
N. But in canonical ensembles
for
N. But in canonical ensembles ![]() , in grand canonical
ensemble
, in grand canonical
ensemble ![]() . Did we cheat?
. Did we cheat?
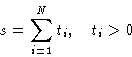
![]()
![]()
![]()
![]()
![]()
![]()
![]()