Next: Equivalence of Ensembles Up: Ensembles and Thermodynamic Potentials Previous: Grand Canonical Ensemble

General Case: How to Introduce a New Ensemble

General Idea

We have an extensive quantity x and the corresponding conjugated variable X:

$\begin{displaymath} X = -\left(\frac{\partial S}{\partial x}\right)_{E,V,N,\dots}\end{displaymath}$

Probability:

$\begin{displaymath} \Prob{A_i} = \frac{1}{Q_x}\exp(Xx_i/kT)\end{displaymath}$

Thermodynamic potential:

$\begin{displaymath} \Omega_x = -kT\ln Q_x = E - xX\end{displaymath}$

$\Omega_x$ is a Legendre transformation of E!

Any conserved extensive quantity generates a conjugated force, ensemble and thermodynamic potential!

We can change volume, but $S=\mathit{const}$ , $N=\mathit{const}$ (infinitely flexible insulated walls)

Extensive variable: V, thermodynamic force: P. Probability of a state:

$\begin{displaymath} \Prob(A_i) = \frac{1}{Q_V}\exp(PV/kT)\end{displaymath}$

Thermodynamic potential:

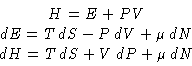
$\begin{displaymath} \begin{gathered} H = E+PV\ dE = T\,dS - P\,dV + \mu\,dN\ dH = T\,dS + V\,dP + \mu\,dN \end{gathered}\end{displaymath}$

H(P,S,N) is enthalpy

Both S and V are not constant.

$\begin{displaymath} \Prob(A_i) = \frac{1}{\Delta}\exp(-E_i/kT+PV/kT)\end{displaymath}$

Gibbs free energy G(P,T,N):

$\begin{displaymath} \begin{gathered} G = -kT\ln\Delta = E -TS +PV\ dG = -T\,dS + V\,dP + \mu\,dN \end{gathered}\end{displaymath}$

Phenomenological Thermodynamics is the study of properties of Legendre transformations of convex functions.
Unknown Mathematician