


Next: Thermodynamic Stability
Up: Maximal Work, Minimal Work
Previous: Maximal Work, Minimal Work
Subsections
So far we discussed reversible processes. What happens for
irreversible ones?
Let us discuss an insulated system (adiabatic process).
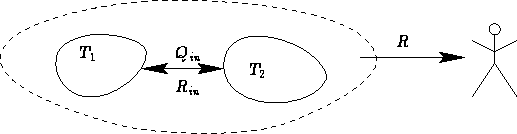
We know the volume of the system in the final state 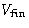 . What
is the maximal work R against the surroundings?
. What
is the maximal work R against the surroundings?
Since there is no heat exchange,
|  |
(1) |
 is given. We want
is given. We want  to be as small as possible (we
are greedy
to be as small as possible (we
are greedy![[*]](/icons/foot_motif.gif) !). Since in
final state the system is in equilibrium,
!). Since in
final state the system is in equilibrium,
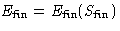 . Differentiate (1):
. Differentiate (1):
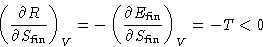
R is a decreasing function of 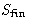 . The lower is
. The lower is
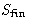 , the better! But S cannot decrease, it can only
increase!
, the better! But S cannot decrease, it can only
increase!
- Conclusion:
- R in a closed system is maximal for
reversible processes, when
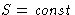
Machines should produce as less entropy as possible!
Consider a not insulated body at temperature T and pressure
P surrounded by environment with temperature T0 and pressure
P0:
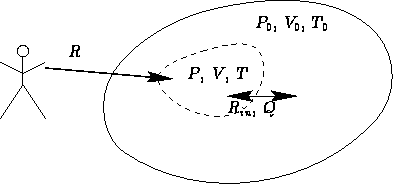
What is the minimal work to change the state of the body 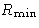 ?
?
- If the source makes work R, the body makes work -R
- Minimal work of the source corresponds to maximal work of
the body
What is the change of energy 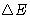 of the body?
of the body?
- Work from the external source R
- Work from the environment
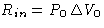
- Heat from the environment
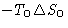
We obtained:
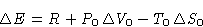
- Since
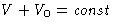 ,
, 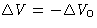
- For reversible processes
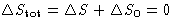 , for irreversible processes
, for irreversible processes 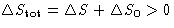 . So
. So 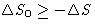
Result:
| 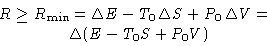 |
(2) |
Particular cases:
Thermodynamic potentials describe the minimal work to produce the
given state at certain external conditions.
Suppose now R=0. We obtained:
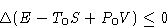
This thing always decreases!
- If T=T0,
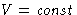 , Helmholtz free energy A decreases,
, Helmholtz free energy A decreases,
- If T=T0, P=P0, Gibbs free energy G decreases,
- If P=P0,
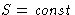 , enthalpy H decreases.
, enthalpy H decreases.
Once again, a body in an environment (microcanonical ensemble):

Let us consider it as a fluctuation: some macroscopic
variable deviated from the mean value. Then 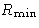 is the
minimal work to create the fluctuation.
is the
minimal work to create the fluctuation.
Probability for the fluctuation is
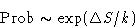
In equilibrium
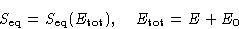
When the system equilibrates, its total entropy increases, so
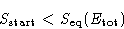
Let 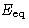 be the energy for which
be the energy for which
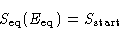
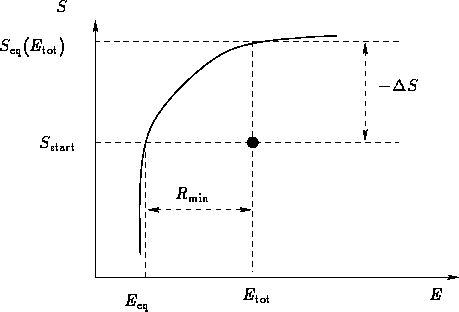
Then:
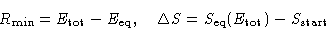
Therefore
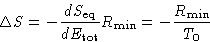
We obtained:
| 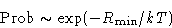 |
(3) |
Difference between (3) and Gibbs formulae: here we discuss
the probability of a macroscopic state!
- Fluctuations at
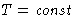 ,
, 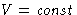 :
: 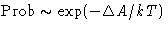
- Fluctuations at
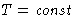 ,
, 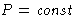 :
: 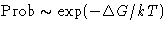
- Fluctuations at
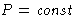 ,
, 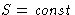
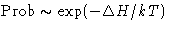



Next: Thermodynamic Stability
Up: Maximal Work, Minimal Work
Previous: Maximal Work, Minimal Work
© 1997
Boris Veytsman
and Michael Kotelyanskii
Fri Sep 12 00:09:21 EDT 1997
![]()
![]()
![]()

![]() . What
is the maximal work R against the surroundings?
. What
is the maximal work R against the surroundings?
![]()

![]() of the body?
of the body?
![]()
![]()
![]()
![]()
![]()

![]() is the
minimal work to create the fluctuation.
is the
minimal work to create the fluctuation.
![]()
![]()
![]()
![]()

![]()
![]()