


Next: Quiz
Up: Maximal Work, Minimal Work
Previous: Maximal and Minimal Work
Subsections
The system is stable if the total entropy  has
maximum. Equivalently,
has
maximum. Equivalently, 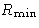 is positive for any
deviation.
is positive for any
deviation.
It means that:
- At
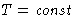 ,
, 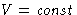 A should be minimal
A should be minimal
- At
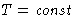 ,
, 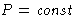 G should be minimal
G should be minimal
- At
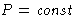 ,
, 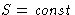 H should be minimal
H should be minimal
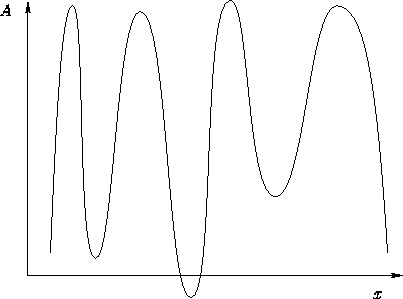
There are two kinds of minima--local and global
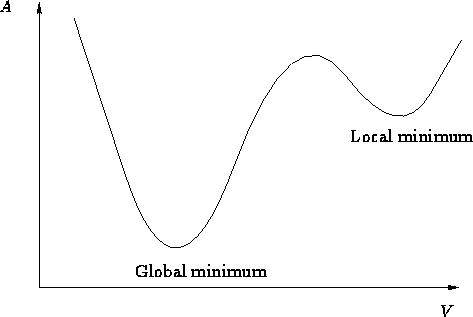
- If the system is neither in a global, nor in a local minimum, it
is unstable
- If the system is in the global minimum, it is stable
- If the system is in the local minimum, it is metastable:
it can spend a lot of time there, but eventually it will leave for
the global minimum. This is called partial equilibrium.
Glasses--many metastable minima:
A body at constant pressure and temperature. Equilibrium
condition: 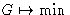
What is the equilibrium volume V for the given pressure?
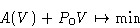
It means that:
- 1.
- First derivative should be zero:
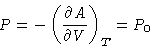
This is mechanical equilibrium condition
- 2.
- Second derivative should be positive:
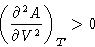
This is convexity condition.
- Definition:
- A function f(x) is convex if f''(x)>0
and concave if f''(x)<0:
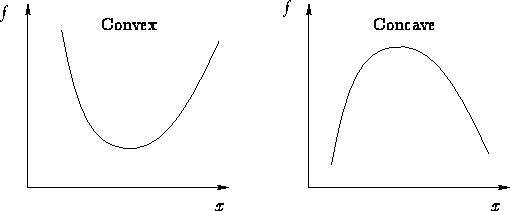
- Mnemonics:
- Concave = ``no coffee''
We proved, that A is a convex function of volume.
If 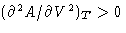 , we can make this point V a
minimum by changing P. If
, we can make this point V a
minimum by changing P. If 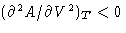 , we
cannot help! Since
, we
cannot help! Since
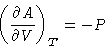
we proved that
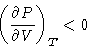
- General Statement:
- Thermodynamic potentials are convex
functions of their extensive arguments.
We now can prove that Legendre Transform of thermodynamic potentials
is always possible!
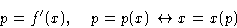
To invert p(x), we need 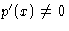 . But this follows from the
convexity condition p'(x)=f''(x)>0!
. But this follows from the
convexity condition p'(x)=f''(x)>0!
- Theorem:
- Thermodynamic potentials are concave functions
of their intensive variables.
- Proof:
- If g(p) is the Legendre transformation of f(x), then
g'(p)=-x and
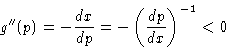
We know the average volume of a given body V0. What is the
probability to obtain V?
We start from the formula:
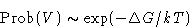
We obtain:
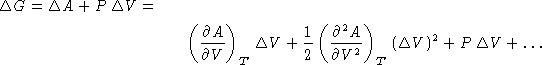
Since
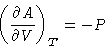
we are left with
![\begin{displaymath}
\Prob(V)\sim\exp\left[ - \frac{1}{2kT}\left(\frac{\partial^2 A}{\partial
V^2}\right)_{T}\,(\Delta V)^2\right]\end{displaymath}](img60.gif)
- Isothermic compressibility:
- We define
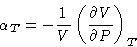
This is an intensive variable (why?).
Then
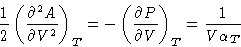
and
![\begin{displaymath}
\Prob(V)=\frac{1}{\sqrt{2\pi kTV \alpha_T}}\exp\left[-\frac{(\Delta
V)^2}{2kT V\alpha_T} \right]\,dV\end{displaymath}](img63.gif)
This is called Gauss Distribution
Average values:
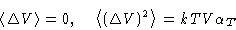
and
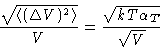
Once again,
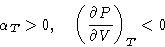
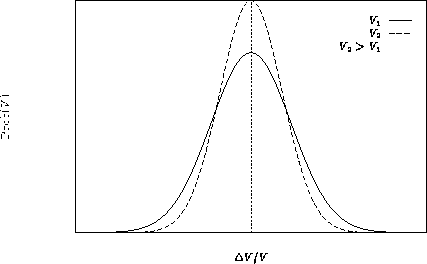
Once again maximal term method: at 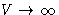 the width becomes zero!
the width becomes zero!



Next: Quiz
Up: Maximal Work, Minimal Work
Previous: Maximal and Minimal Work
© 1997
Boris Veytsman
and Michael Kotelyanskii
Fri Sep 12 00:09:21 EDT 1997
![]()
![]()
![]()
![]() has
maximum. Equivalently,
has
maximum. Equivalently, ![]() is positive for any
deviation.
is positive for any
deviation.


![]()
![]()
![]()
![]()

![]() , we can make this point V a
minimum by changing P. If
, we can make this point V a
minimum by changing P. If ![]() , we
cannot help! Since
, we
cannot help! Since
![]()
![]()
![]()
![]()
![]()
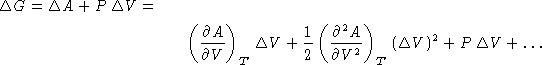
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() the width becomes zero!
the width becomes zero!