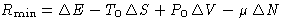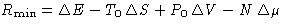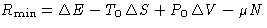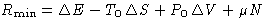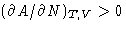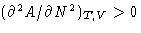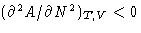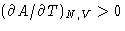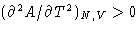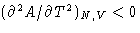Up: Maximal Work, Minimal Work
Previous: Thermodynamic Stability
- 1.
- In equation (2) we implicitly assumed
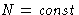 . If
the number of particles changes, the correct expression for
. If
the number of particles changes, the correct expression for
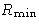 should be:
should be:
- (a)
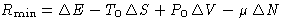
- (b)
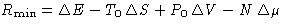
- (c)
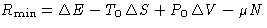
- (d)
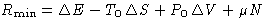
- 2.
- From the convexity condition follows (check all right
statements):
- (a)
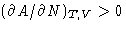
- (b)
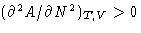
- (c)
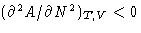
- (d)
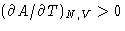
- (e)
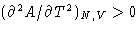
- (f)
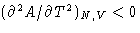
© 1997
Boris Veytsman
and Michael Kotelyanskii
Fri Sep 12 00:09:21 EDT 1997