


Next: Phase Transitions
Up: Thermodynamics of Phase Transitions
Previous: Thermodynamics of Phase Transitions
Subsections
- 1.
- Draw a plot of the single particle distribution function
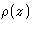 as a function of z for the liquid monolayer, adsorbed
on the flat surface. z is the distance perpendicular to the
adsorbing surface. Consider a liquid of hard-spheres of diameter
d.
as a function of z for the liquid monolayer, adsorbed
on the flat surface. z is the distance perpendicular to the
adsorbing surface. Consider a liquid of hard-spheres of diameter
d.
- Solution:
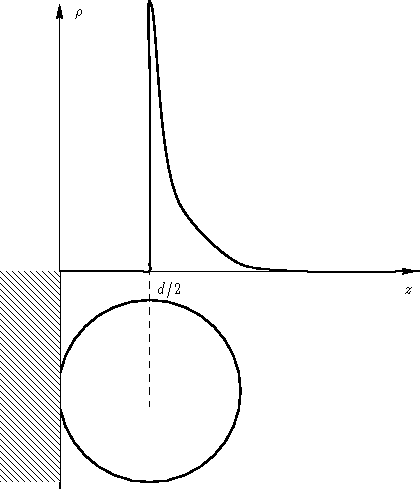
- There are molecules at the distance d/2 from the
wall only (we have a monolayer), so
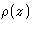 has a sharp
peak:
has a sharp
peak:
- 2.
- How is
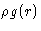 normalized?
normalized?
- Solution:
- The expression
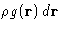 is the average
number of particles in the volume
is the average
number of particles in the volume 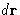 around the point
around the point 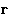 if one particle is in the point
if one particle is in the point 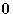 . Integrating this,
we obtain N-1 (one particle is at the point
. Integrating this,
we obtain N-1 (one particle is at the point 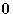 !).
!).
- 3.
- Does
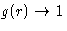 at large distances in the perfect crystal?
at large distances in the perfect crystal?
- Solution:
- The function
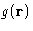 does not. Crystal has
long range order:
does not. Crystal has
long range order:
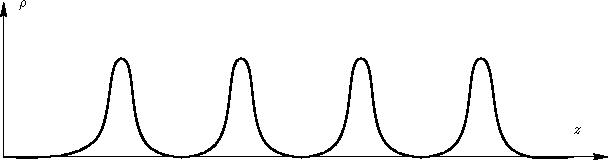
When we average integrate over 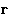 , we obtain many peaks,
but they do not tend to 1.
, we obtain many peaks,
but they do not tend to 1.
- 4.
- Is the derivation of the equations (3-9)
valid for the anisotropic liquid crystals, or for crystalline
solids?
- Solution:
- As long as we don't introduce spherical symmetry
and integrate over dr, our equations are valid
- 1.
- Equipartition theorem works
- (a)
- For high temperatures
- (b)
- For low temperatures
- (c)
- Always
- (d)
- Never
- Solution:
- Since classical limit is for high temperatures
(difference between levels
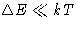 ), the
answer (1a) is right
), the
answer (1a) is right
- 2.
- Consider a cubic crystal with
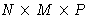 atoms,
N<M<P. The minimal value of q is
atoms,
N<M<P. The minimal value of q is
- (a)
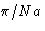
- (b)
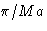
- (c)
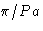
- (d)
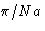
- (e)
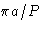
- (f)
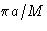
- (g)
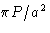
- (h)
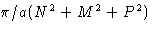
- Solution:
- The values for
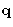 are
are
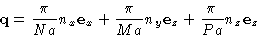
where 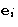 is the unit vector along the corresponding
axis. Then
is the unit vector along the corresponding
axis. Then
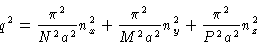
This is minimal at nx=ny=0, nz=1. The correct answer
is (2c).
- 1.
- Sketch the phase diagram for two phase equilibrium in P-T
and V-T coordinates.
- Solution:
- Since P is an intensive parameter, and V is an
extensive one, we have:
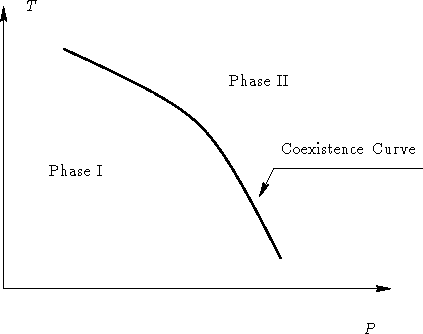
and in V-T space:
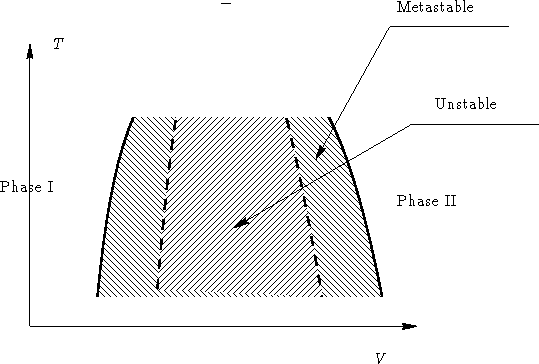
- 2.
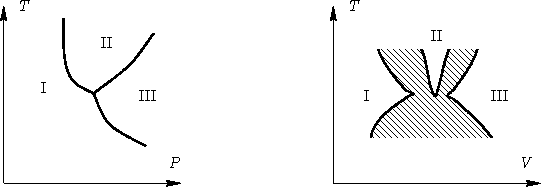
- Same near triple point.
- Solution:
- See picture:
- 3.
- Consider a one-component system in an external electric field
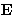 . It can have dipole moment
. It can have dipole moment 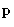 parallel to
parallel to
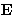 . How many phases can coexist in this system?
. How many phases can coexist in this system?
- Solution:
- We add a scalar parameter |E|. Therefore the number
of phases is 3+1=4.
- 4.
- Same for binary blend in electric field.
- Solution:
- 5 (see above)



Next: Phase Transitions
Up: Thermodynamics of Phase Transitions
Previous: Thermodynamics of Phase Transitions
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 7 22:16:36 EDT 1997
![]()
![]()
![]()


![]()
![]()


