


Next: Phase Transitions in Van
Up: Thermodynamics of Phase Transitions
Previous: Quiz Answers
Subsections
Take a sample of phase I and slowly transform it into phase
II. Some heat Q will be absorbed.
- Since this is reversible,
| 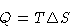 |
(1) |
- Since in equilibrium P1=P2, the process occurs at constant
pressure
- Since T1=T2, it occurs at constant temperature
We have
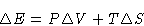
or
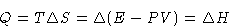
The heat of phase transition is equal to the change of enthalpy.
On the P-T diagram phase transition occur along a line
P(T). Let's calculate the tangent to this line dP/dT.
Chemical potentials are equal:
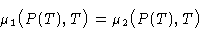
Differentiating:
| 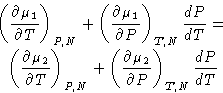 |
(2) |
We know from previous
lectures
that
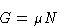
and therefore
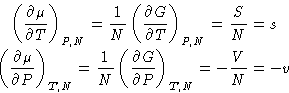
with s and v being quantities per molecule
From (2):
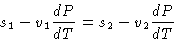
or
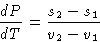
Since
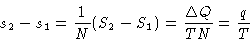
we obtained
| 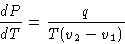 |
(3) |
This is Clapeyron-Clausius equation
- For liquid-gas phase transitions q>0. Since v2>v1,
dT/dP= (dP/dT)-1>0. Boiling point temperature
increases with pressure
- For solid-liquid phase transitions q>0 (exception:
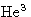 ). Usually v2>v1, and melting point increases
with pressure. For water v2<v1, and it
decreases--that is why skating & skiing is possible!
). Usually v2>v1, and melting point increases
with pressure. For water v2<v1, and it
decreases--that is why skating & skiing is possible!
Assumptions:
- 1.
- Phase transition heat q does not depend on T and P:
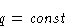
- 2.
- Gas is ideal (PV=NkT), and its volume is much grater than of
liquid:
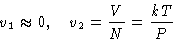
We obtain:
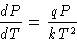
or
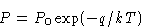
If we move from phase I to phase II, thermodynamic potential G
is continuous (why?), but its first derivative S
jumps. Another possibility: S is continuous, but 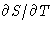 jumps.
jumps.
- Definition:
- if the n-th derivative of free energy
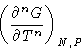
is discontinuous, and all lower derivatives are not, the transition
is of n-th order.
- Phase equilibrium:
- first order phase transition!
- Second order phase transitions:
- Curie point, some
liquid crystal phase transitions...
- Practical guide:
- if q=0, the transition is of the second
order (or higher!).
- First-order-close-to-second-order transitions:
- q small
(liquid crystals)



Next: Phase Transitions in Van
Up: Thermodynamics of Phase Transitions
Previous: Quiz Answers
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 7 22:16:36 EDT 1997
![]()
![]()
![]()
![]()
![]()
![]()
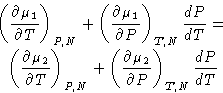
![]()
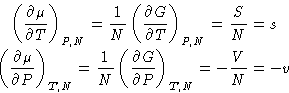
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() jumps.
jumps.
![]()