


Next: Quiz
Up: Thermodynamics of Phase Transitions
Previous: Phase Transitions
Subsections
We know from previous
lectures
:
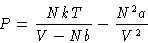
Stability condition:
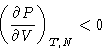
Is this always true for VdW gas?
| 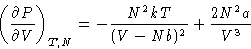 |
(4) |
- 1.
- If T is large enough, the first term in (4)
dominates--system is always stable
- 2.
- If T is small, first term wins only for
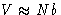 and
and
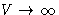 --system is unstable at intermediate V!
--system is unstable at intermediate V!
- 3.
- Borderline case:
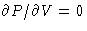 just in one point
(critical point K)
just in one point
(critical point K)
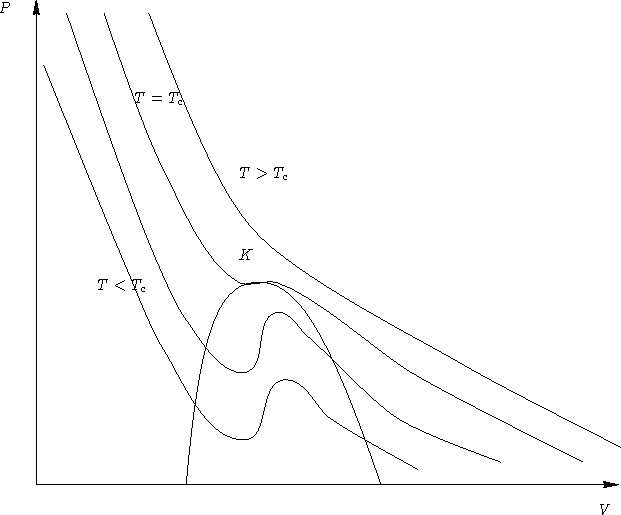
Phases:
- 1.
- At T>Tc one phase (fluid)--no phase transitions
- 2.
- At T<Tc two phases (liquid & gas)--first order phase
transition
- 3.
- At T=Tc--second order phase transition
Equation for Tc:
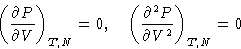
or
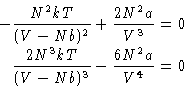
Result:
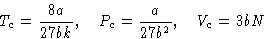
Let us measure everything in critical units:
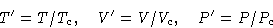
Van der Waals law:
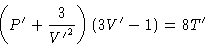
This is same for all van der Waals gases! All PVT data lie on same
master curve. This is called law of corresponding states.
Let us determine binodal for van der Waals gas. In coexisting phases
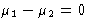 or
or
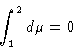
If 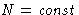 ,
, 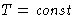 we have
we have 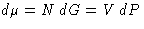 , or
, or
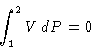
It means that dashed areas below are equal!
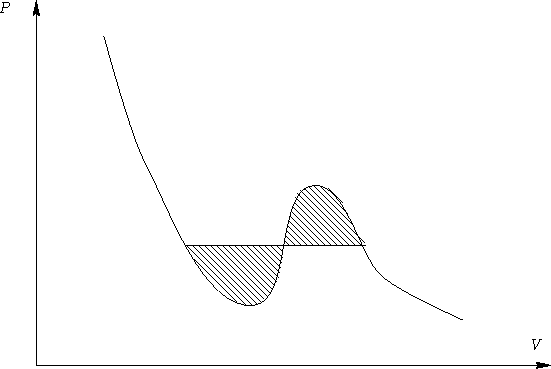



Next: Quiz
Up: Thermodynamics of Phase Transitions
Previous: Phase Transitions
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 7 22:16:36 EDT 1997
![]()
![]()
![]()
![]()
![]()

![]()
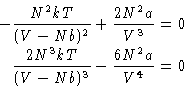
![]()
![]()
![]()
![]() or
or
![]()
![]()
