Next: Conclusion Up: Ising Model and Its Previous: Phase Transitions of Ising
![]()
![]()
![]()
Next: Conclusion
Up: Ising Model and Its
Previous: Phase Transitions of Ising
Ising model was invented to describe phase transition in magnetics. It also describes gas-liquid phase transition!
Consider a lattice model:
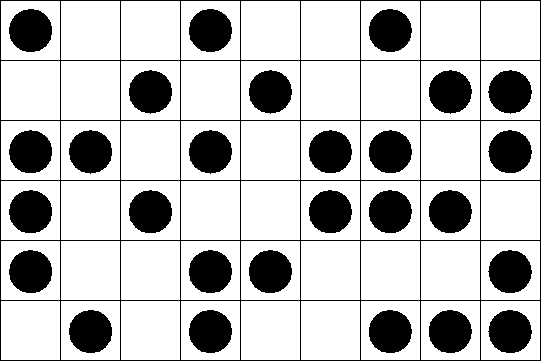
Each site can be either occupied or empty. Only nearest neighbors
interact. Energy of interaction ![]() . We want to map this to
Ising model. Introduce a spin
. We want to map this to
Ising model. Introduce a spin
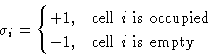
Number of particles in a cell:
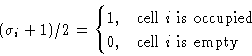
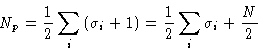
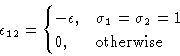
![]()
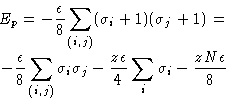
| |
(2) |
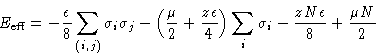
![]()
| Ising Magnetic | Lattice Gas |
| Canonical ensemble | Grand canonical ensemble |
| Coupling constant J | Interaction energy |
| External field H | Chemical potential |
| Magnetization M | Density |
| Free energy A | |
| Susceptibility |
Compressibility |
| Isotropic phase | Supercritical fluid |
| Ordered phase | Liquid or gas |
| Curie point | Critical point |
An incompressible mixture of A and B:
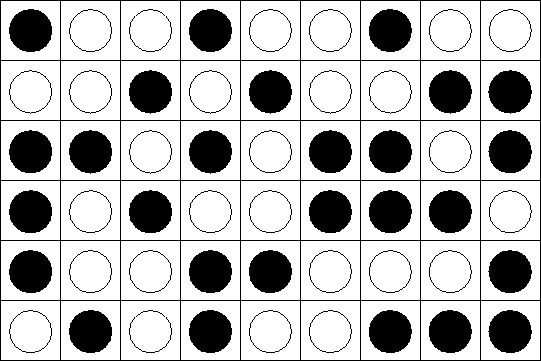
Once again, only closest neighbor interact. Energy of
interaction![]() :
:

We introduce spins:
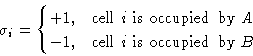
![]()
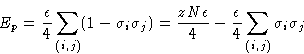
![]()
I cannot use grand canonical ensemble: the total # of particles is constant (incompressibility). Semi-Grand Ensemble: the total number of particle is constant, but I can switch A and B.
Partition function:
![]()
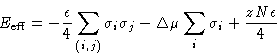
![]()
Correspondence between Ising magnetic & binary mixture:
| Ising Magnetic | Binary Mixture |
| Canonical ensemble | Semi-grand canonical ensemble |
| Coupling constant J | Interaction energy |
| External field H | Chemical potential diff. |
| Magnetization M | Composition |
| Isotropic phase | Mixed phase |
| Ordered phase | Separated phase |
| Curie point | Critical mixing point |
How can we extend Ising model?
© 1997 Boris Veytsman and Michael Kotelyanskii