Next: Self-Consistent Field Theory Up: Mean Field Approach Previous: General Idea

Flory Theory

Approximation

Lattice gas analogy--we have N cells, N_p particles A and N-N_p particles B. We will use canonical ensemble (Ising model for magnetics corresponds to grand canonical ensemble!). Partition function:

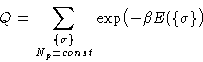$\begin{displaymath} Q = \sum_{\substack{\{\sigma\}\ N_p=\mathit{const}}} \exp\bigl(-\beta E(\{\sigma\}\bigr) \end{displaymath}$ (1)

Flory idea: substitute (1) by

$\begin{displaymath} Q\approx\mathcal{N}\exp\bigl(-\beta\left\langle E\right\rangle\bigr) \end{displaymath}$

Free Energy

The number of terms

$\begin{displaymath} \mathcal{N} = \frac{N!}{N_p!(N-N_p)!}\end{displaymath}$

Average energy: we have N_p As. Each A has z neighbors. About N_pz/N of them are A, (N-N_p)z/N are B. We have

$\begin{displaymath} \left\langle E\right\rangle = \frac{z\epsilon N_p(N-N_p)}{N}\end{displaymath}$

Free energy:

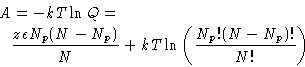$\begin{displaymath} \begin{split} A &= -kT\ln Q =\ & \frac{z\epsilon N_p(N-N_p)}{N} + kT\ln\left(\frac{N_p!(N-N_p)!}{N!} \right) \end{split}\end{displaymath}$

(2)

Stirling formula:

$\begin{displaymath} \ln N!\approx N\ln N - N,\quad N\gg1\end{displaymath}$

New variables:

$\begin{displaymath} \phi = \frac{N_p}{N},\quad \chi_F = \frac{z\epsilon}{kT}\end{displaymath}$

Free energy:

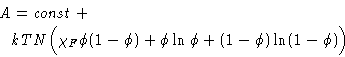$\begin{displaymath} \begin{split} A &= \mathit{const}+\ & kTN\Bigl(\chi_F\phi(1-\phi) + \phi\ln\phi + (1-\phi)\ln(1-\phi)\Bigr) \end{split} \end{displaymath}$

(3)

Critical Point

System is symmetric--critical point is at $\phi=1/2$ . We obtain

$\begin{displaymath} \frac{\partial^2 A}{\partial\phi^2} = 0\end{displaymath}$

$\begin{displaymath} \frac{1}{\phi} + \frac{1}{1-\phi} - 2\chi_F = 0\end{displaymath}$

which gives

$\begin{displaymath} \chi_F = \frac{z\epsilon}{kT} = 2\end{displaymath}$

The system is mixed above critical point and demixed below it

Binodal & Spinodal

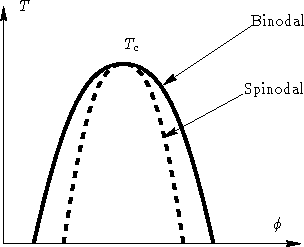
Free energy of Flory system below critical point
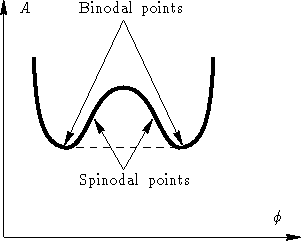
$\begin{figure} \psfrag{A}{$A$} \psfrag{phi}{$\phi$} \psfrag{Binodal points}{B... ...rag{Spinodal points}{Spinodal points} \includegraphics{free_energy}\end{figure}$
On spinodal the second derivative is zero:

$\begin{displaymath} \frac{1}{\phi} + \frac{1}{1-\phi} - 2\chi_F = 0\end{displaymath}$

On binodal there is local minimum--first derivative is zero:

$\begin{displaymath} \ln\phi - (1-\phi)\ln(1-\phi) + \chi_F(1-2\phi) = 0\end{displaymath}$

In critical point binodal & spinodal coincide:
$\begin{figure} \psfrag{T}{$T$} \psfrag{Tc}{$T_c$} \psfrag{phi}{$\phi$} \psfr... ...nodal} \psfrag{Spinodal}{Spinodal} \includegraphics{phase_diagram}\end{figure}$

Problems of Flory Theory

1.

It is not clear how to calculate next approximation(s)

2.

Works because of compensation of errors:

We overestimate $\left\langle E\right\rangle$ : correlations decrease average energy
We overestimate $\mathcal{N}$ : most of states have too small contribution to Q

Flory theory overestimates both energy and entropy--the resulting expression is ``more or less'' right.

Next: Self-Consistent Field Theory Up: Mean Field Approach Previous: General Idea