


Next: Landau Theory
Up: Mean Field Approach
Previous: Flory Theory
Subsections
Energy of Ising system is
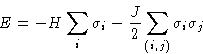
It can be written as

with molecular field
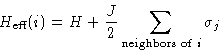
We substitute 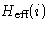 by its average value
by its average value
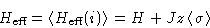
and choose 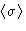 from consistency condition!
from consistency condition!
Let us write
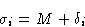
The product:
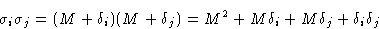
Approximation: neglect 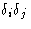 . Result:
. Result:
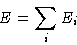
with
| 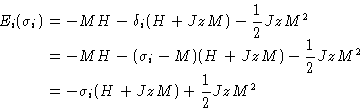 |
(4) |
We separated energy into independent contributions from each spin!
Partition function:
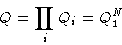
Partition function for one spin
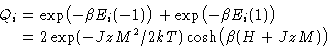
Free energy:
| 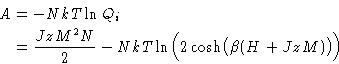 |
(5) |
This depends on the magnetization M!
There are two ways to calculate M:
By definition, 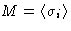 . Since only Ei depends on
. Since only Ei depends on
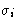 , we have:
, we have:
![\begin{displaymath}
M = \frac{1}{Q_i}\left[\exp\bigl(-\beta E_i(1)\bigr) - \exp\bigl(-\beta
E_i(-1)\bigr) \right]\end{displaymath}](img34.gif)
or, from (4)
| 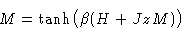 |
(6) |
This is a transcendent equation for M.
Free energy (5) depends on M. It should be minimal as
function of M:
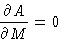
or
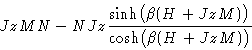
This gives
| 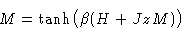 |
(7) |
The results (6) and (7) coincide! Our theory is
self-consistent.
We can rewrite equation (7) as
| 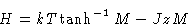 |
(8) |
- 1.
- At large T, this is monotonic function:
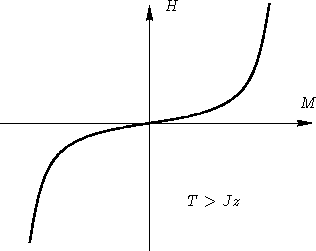
This means one-phase regime
- 2.
- At low T, this is non-monotonic function:
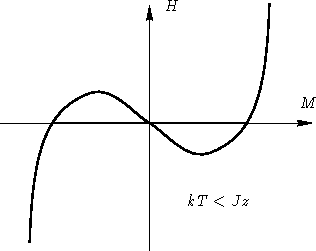
From stability condition 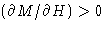 we see, that
this means phase separation
we see, that
this means phase separation
- 3.
- At critical temperature Tc, we have only one point, where
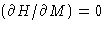 :
:
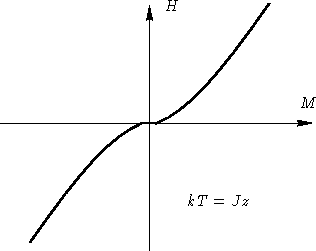
At this temperature
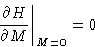
or, from (8)
kT=Jz
Phase diagram:
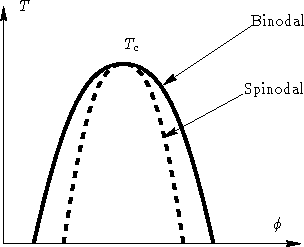
- Give same critical point
- Expansions near critical point coincide up to quadratic terms
- Give different results farther from critical point
Advantages of SCF:
- 1.
- We know how to extend it--just make a better approximation for
 .
. - 2.
- Works better farther from critical point



Next: Landau Theory
Up: Mean Field Approach
Previous: Flory Theory
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 14 22:58:59 EDT 1997
![]()
![]()
![]()
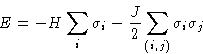
![]()
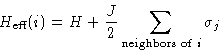
![]()
![]()
![]()
![]()
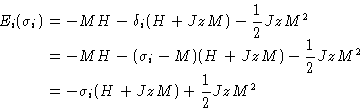
![]()
![]()
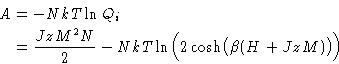
![]() . Since only Ei depends on
. Since only Ei depends on
![]() , we have:
, we have:
![]()
![]()
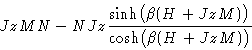

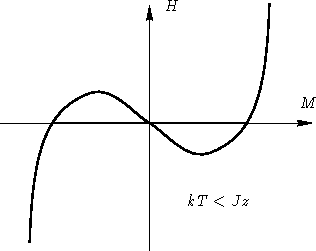
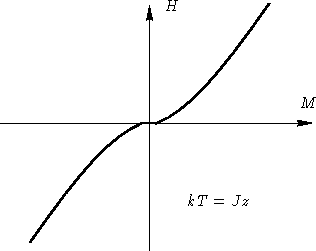
![]()
