


Next: Quiz
Up: Mean Field Approach
Previous: Self-Consistent Field Theory
Subsections
From previous section we learned that:
- 1.
- Free energy A is an analytical function of
magnetization M
- 2.
- At T>Tc it has one minimum, at T<Tc--two
Landau idea: let us use only these facts!
Let us expand free energy A in powers of M.
First, a symmetric system: H=0. Then M=0 is
either a minimum (T>Tc) or a maximum (T<Tc) of the free
energy. Due to symmetry only even powers are present:
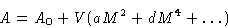
- Assumption:
- We neglect all powers higher than 4.
At large 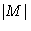 free energy should be large--so d>0. We will
see below that at a>0 there is one phase, at a<0--two. So a
should change sign at T=Tc. We will expand it:
free energy should be large--so d>0. We will
see below that at a>0 there is one phase, at a<0--two. So a
should change sign at T=Tc. We will expand it:
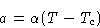
With the same accuracy:
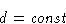
Result:
| 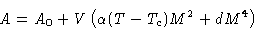 |
(9) |
Differentiate (9):
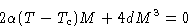
Solutions:
| 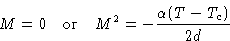 |
(10) |
At T>Tc only the first solution is realized--one phase. At T<Tc we
have two solutions--two phases:
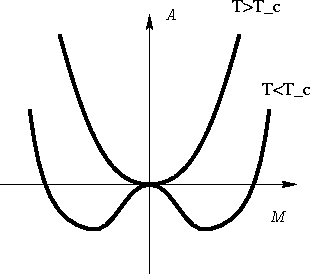
Equation of binodal is (10):
| 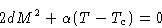 |
(11) |
This is parabola.
Equation of spinodal: 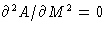 or
or
| 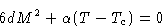 |
(12) |
This is another parabola, inside the binodal
Free energy:
| 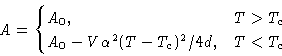 |
(13) |
Entropy is
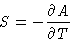
Differentiating (13):
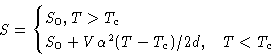
Specific heat:
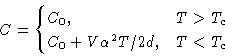
There is a jump in specific heat near Tc:
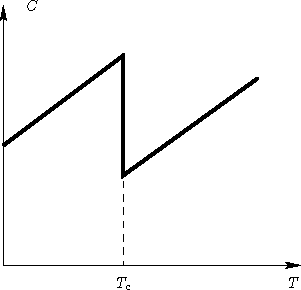
Now we add a small external field H:
| 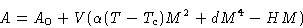 |
(14) |
and want to calculate
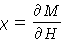
Minimizing (14):
| 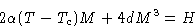 |
(15) |
Two cases:
- 1.
- If T>Tc, then M(H=0)=0. For small H we neglect M3, and
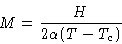
Susceptibility
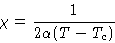
This diverges at 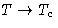 .
. - 2.
- If T<Tc, then
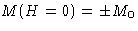 with
with 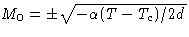 . Let
. Let
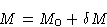
Expanding (15), we obtain
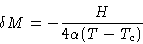
and
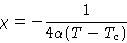
This also diverges
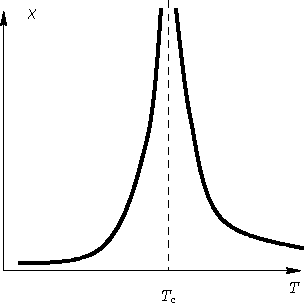
We obtained a  -like curve:
-like curve:



Next: Quiz
Up: Mean Field Approach
Previous: Self-Consistent Field Theory
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Oct 14 22:58:59 EDT 1997
![]()
![]()
![]()
![]()
![]()
![]()
![]()

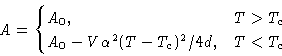
![]()
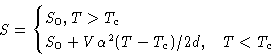
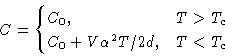
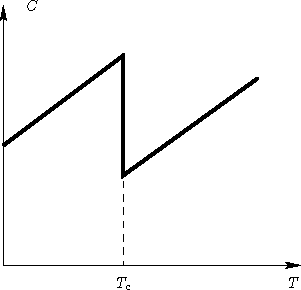
![]()
![]()
![]()
![]()
![]()
![]()
![]() -like curve:
-like curve:
