Next: Interface Layer in Landau Up: Spatial Inhomogeneity. Interfaces Previous: Landau Theory
![]()
![]()
![]()
Next: Interface Layer in Landau
Up: Spatial Inhomogeneity. Interfaces
Previous: Landau Theory
Suppose we want to minimize the function:
| |
(4) |
![]()
Standard calculus: if we want to minimize y(x), we consider a small deviation:
![]()
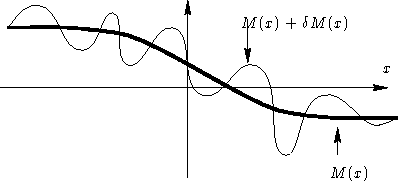
In this situation we have a functional ![]() that
depends on the function M(x). Same idea: consider a
deviation:
that
depends on the function M(x). Same idea: consider a
deviation:
![]()
![]()
![]()
![]()
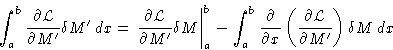
![]()
| |
(5) |