Next: Quiz Up: Spatial Inhomogeneity. Interfaces Previous: Mathematical Digression: Euler-Lagrange Equation
![]()
![]()
![]()
Next: Quiz
Up: Spatial Inhomogeneity. Interfaces
Previous: Mathematical Digression: Euler-Lagrange Equation
We need to minimize the functional
![\begin{displaymath}
\begin{split}
&A = A_0+ \\ & W\int\left[aM^2+dM^4-HM+g\left(\frac{\partial
M}{\partial x}\right)^2\right]\,dx
\end{split}\end{displaymath}](img23.gif)
![]()
![]()
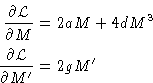
| gM''=aM+2dM3 | (6) |
Multiply (6) by M'. Then
![]()
![]()
![]()
![]()
To find C note that at ![]() we have
we have
![]()
![]()
![]()
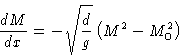 |
(7) |
![]()
| |
(8) |
| |
(9) |
In the bulk the energy per unit volume is
![]()
![]()
![]()
![]()
![]()
| |
(10) |
What happens at ![]() ? Coefficient a tends to zero as
? Coefficient a tends to zero as
![]() .
.
![]()
As we are closer to the critical point, the interface layer becomes
thicker, and the surface tension drops. Since ![]() ,
correlation length diverges, and
,
correlation length diverges, and ![]() means that the
difference between the phases disappears. The penalty for forming
interface becomes lower, and fluctuations grow.
means that the
difference between the phases disappears. The penalty for forming
interface becomes lower, and fluctuations grow.
© 1997 Boris Veytsman and Michael Kotelyanskii