


Next: Mathematical Digression: Euler-Lagrange Equation
Up: Spatial Inhomogeneity. Interfaces
Previous: Self-Consistent Field Theory
Subsections
In homogeneous phase we had
![\begin{displaymath}
A = A_0+V\left[aM^2+dM^4-HM\right]\end{displaymath}](img16.gif)
Now we divide system into layers, and
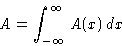
with A(x) being the free energy of one layer.
We want to add the dependence on 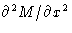 . Lowest order: linear dependence on
. Lowest order: linear dependence on 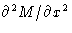 . But this is not symmetric with respect to
. But this is not symmetric with respect to
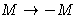 . Solution: use
. Solution: use
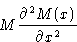
Integrating by parts:
| 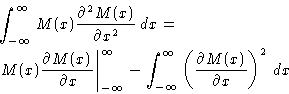 |
(2) |
If there is bulk phase at 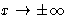 , first term is
zero. Otherwise we can include it in the boundary conditions. Result:
, first term is
zero. Otherwise we can include it in the boundary conditions. Result:
![\begin{displaymath}
\begin{split}
&A = A_0+ \\ & W\int\left[aM^2+dM^4-HM+g\left(\frac{\partial
M}{\partial x}\right)^2\right]\,dx
\end{split}\end{displaymath}](img23.gif)
where W is the cross-section normal to x
General case: substitute 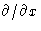 by
by  :
:
| ![\begin{displaymath}
A= A_0 + \int\left[aM^2+dM^4-HM+g\left(\nabla M\right)^2\right]\,d\mathbf{r}\end{displaymath}](img26.gif) |
(3) |
The term 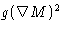 is called Lifshits term, and free
energy (3)--Landau Hamiltonian (or Landau-Ginsburg
Hamiltonian).
is called Lifshits term, and free
energy (3)--Landau Hamiltonian (or Landau-Ginsburg
Hamiltonian).
- 1.
- Sign of g: if g<0, ``wavy'' structures are favored:
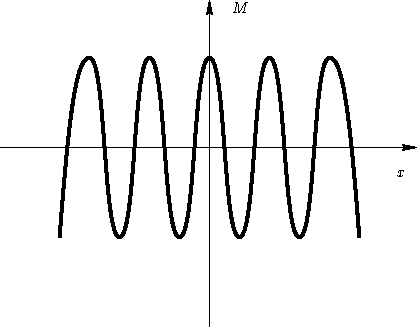
Therefore g>0.
- 2.
- Value of g: the dimensionality of g/d is
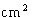 (Why?). From previous section it is clear, that this of the
order of the
square of the molecular size a0:
(Why?). From previous section it is clear, that this of the
order of the
square of the molecular size a0:
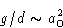
Since 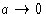 at
at 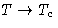 , we obtain
, we obtain 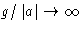 . We
will see that this is square of the correlation length:
. We
will see that this is square of the correlation length:
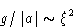



Next: Mathematical Digression: Euler-Lagrange Equation
Up: Spatial Inhomogeneity. Interfaces
Previous: Self-Consistent Field Theory
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Oct 16 20:58:44 EDT 1997
![]()
![]()
![]()
![]()
![]()
![]() . Lowest order: linear dependence on
. Lowest order: linear dependence on ![]() . But this is not symmetric with respect to
. But this is not symmetric with respect to
![]() . Solution: use
. Solution: use
![]()
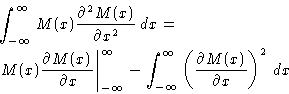
![\begin{displaymath}
\begin{split}
&A = A_0+ \\ & W\int\left[aM^2+dM^4-HM+g\left(\frac{\partial
M}{\partial x}\right)^2\right]\,dx
\end{split}\end{displaymath}](img23.gif)

![]()
![]()