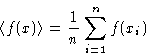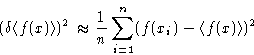Next: Importance Sampling. Metropolis Algorithm
Up: Importance Sampling. Monte Carlo
Previous: Importance Sampling. Monte Carlo
- Classical System:
- Phase Space
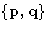
![[*]](/icons/foot_motif.gif)
- Distribution function for the NVT-ensemble:
-
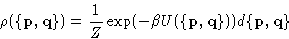
- Ensemble Average for the quantity
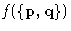 :
:
-
| 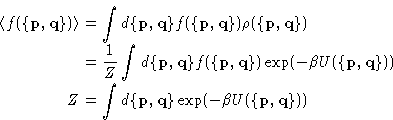 |
(1) |
Unless explicitly stated,
below we always assume, that kinetic energy is separable, and therefore,
we care about the configurational  3N-dimensional space.
The contribution from the momentum part is trivial, and can be
taken into account a posteriori.
3N-dimensional space.
The contribution from the momentum part is trivial, and can be
taken into account a posteriori.
- Brute Force Approach:
- We can try to calculate the integrals in (1)
directly.
It works for simple systems, like the Harmonic oscillator
for instance.
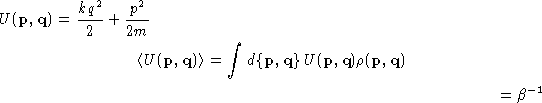
Or we can calculate it numerically using e.g. Simpson's rule,
if the energy function is more complex.
But if it's a system of the N particles, integrals are over the
6N dimensional space and we would have to evaluate the function
at the grid of 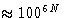 points!!!!
points!!!!
- Monte Carlo method for calculating integrals:
- An integral of a function f(x) on the interval [a,b]
can be represented as:
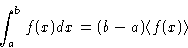
This is a key to the Monte Carlo method for calculating integrals:
- 1.
- throw n points at random positions xi within the interval
(or region for the multi-dimensional case)
- 2.
- calculate the average
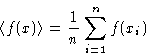
- 3.
- accuracy of the average is estimated by calculating the deviation:
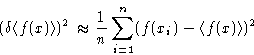
- Fortran code Example 1 :
- Here is an
example of the Fortran code to calculate integral of the x2 from
to 1 by Monte Carlo method
![[*]](/icons/foot_motif.gif) .
Code.
.
Code.



Next: Importance Sampling. Metropolis Algorithm
Up: Importance Sampling. Monte Carlo
Previous: Importance Sampling. Monte Carlo
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Nov 4 23:48:52 EST 1997
![]()
![]()
![]()
![]()
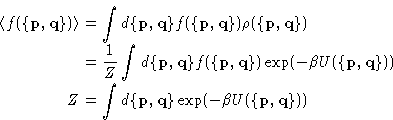
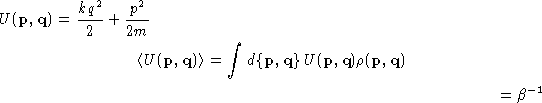
![]() points!!!!
points!!!!
![]()