Importance Sampling. Metropolis Algorithm

Ensemble distribution is sharply peaked in some regions of the phase space, and is very small, virtually zero in the most of it.

For liquid, for instance, only the configurations without overlaps are possible. That means, that applying simple Monte Carlo approach to our problems is not very helpful.

The cure is to sample the relevant configurations only. We can create a random walk in the phase space, sampling it with the ensemble distribution.

$$\rho(\{\mathbf{q}\})=\frac{1}{Z}\exp(-\beta U(\{\mathbf{q}\})$$

Then, the ensemble average, would be just the average over all points $\{\mathbf{q}\}_i$, generated by this random walk:
$$\begin{multline*} \langle f(\{\mathbf{q}\})\rangle = \int d\{\mathbf{q}\} f(\{\m... ...o(\{\mathbf{q}\}) \ = \sum_{\{\mathbf{q}\}_i}f(\{\mathbf{q}\}_i)\end{multline*}$$

Designing the random walk algorithm:

We want our random walk to sample phase space with the probability density $P\sim\exp(-\beta U)$

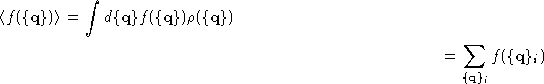
Designing a random walk means to specify the algorithm to go from the current point $\{\mathbf{q}\}$ to the next $\{\mathbf{q}\}'$. If the transition probability to go from $\{\mathbf{q}\}$ to $\{\mathbf{q}\}'$ in one step is $W(\{\mathbf{q}\}\rightarrow\{\mathbf{q}\}')$, and the probability density at the n-th step is $P(\{\mathbf{q}\},n)$, we can write the ``master equation'' for our random walk:

$$\begin{aligned} P(\{\mathbf{q}\},n+1) &= P(\{\mathbf{q}\},n... ...'\rightarrow\{\mathbf{q}\}) P(\{\mathbf{q}\}',n) \end{aligned}$$

It is the same equation as the Kolmogorov-Chapman equation from the last lecture . It's called differently, because, unlike the situation in the last lecture, here we know P, and try to find W. This equation just counts the probability to be at the point $\{\mathbf{q}\}$ at the n+1-st step as the probability to be there at the n-th step minus the probability to leave for any other point $\{\mathbf{q}\}'$, plus the probability to come from any other point $\{\mathbf{q}\}'$. As we want to build the stationary random process, we do not want P depend on n, hence we assume $P(\{\mathbf{q}\},n+1) = P(\{\mathbf{q}\},n)$. We also use that $P=\exp(-\beta U)/Z$. 

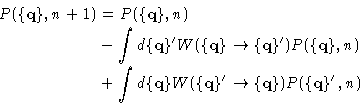
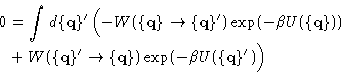$$\begin{aligned} 0 &= \int d\{\mathbf{q}\}' \, \Bigl( - W(\... ...\mathbf{q}\}) \exp(-\beta U(\{\mathbf{q}\}')\Bigr)\end{aligned}$$ (2)

Any random process with the transition probability satisfying equation (2) would serve our purpose, but we want to go the easy way. We'll try to construct the random walk, that satisfies more strict condition of the detailed balance. Instead of solving the integral equation for W, we make W satisfy the following:

• For any two points $\{\mathbf{q}\}$ and $\{\mathbf{q}\}'$  

  $$\begin{split} W(\{\mathbf{q}\}&\rightarrow\{\mathbf{q}\}') ... ...arrow\{\mathbf{q}\}) \exp(-\beta U(\{\mathbf{q}\}'))\end{split}$$ (3)

Detailed balance is a sufficient, but not necessary condition for a random process to sample the phase space with the probability density $P\sim\exp(-\beta U)$. Any scheme, satisfying (3) will do it for sure, but it does not mean, that if a random process does not satisfy (3), it's probability density P cannot be proportional to $\exp(-\beta U)$.

There is more than one solution for W to satisfy detailed balance. Most of the MC methods do so, as this is the safest way to make a Monte Carlo simulation. It guarantees success..

Here are two examples ($\delta U= U(\{\mathbf{q}\}')-U(\{\mathbf{q}\})$)

1.

$$W(\{\mathbf{q}\}\rightarrow\{\mathbf{q}\}') = \frac{1}{\tau}\cdot\frac{\exp(-\beta \delta U)}{1+\exp(-\beta \delta U)}$$

2.

 

$$W(\{\mathbf{q}\}\rightarrow\{\mathbf{q}\}') = \begin{cases... ...au, & \delta U \gt 0 \ 1/\tau, & \delta U \leq 0 \end{cases}$$ (4)

$1/\tau$ is an arbitrary constant. If there is any dynamic interpretation of the MC simulation, $\tau$ can be taken as a time scale corresponding to one MC step. The second example (4) is the basis of the famous Metropolis Monte Carlo algorithm

Metropolis algorithm:

Here is how it goes:

1.

Choose the initial position, calculate energy

2.

Pick the random displacement, calculate the new location and energy

3.

Decide whether to accept the move:

• if $\delta U \gt 0$, calculate $w=\exp(-\beta \delta U)$
• draw a random number r from 0 to 1.
• if w<r or $\delta U \leq 0$, accept the new position, update it and the energy, otherwise, stay at the same place, add the current values to the running averages.

4.

go back to step 2

Fortran code Example 2 :

Here is an example of the Fortran code to calculate the average energy for the harmonic oscillator by the Metropolis Monte Carlo method. Code.