


Next: Quiz
Up: Off-lattice Monte-Carlo Simulations. Lennard-Jones
Previous: Off-Lattice MC algorithm for
Now we have to show that this algorithm does satisfy
the detailed balance condition:
| 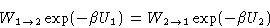 |
(2) |
where 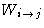 is a probability to go from the micro-state
i to the micro-state j. In our case the micro-states 1
and 2 differ by the position of one particle, that is moved at a
single MC step. The probability
is a probability to go from the micro-state
i to the micro-state j. In our case the micro-states 1
and 2 differ by the position of one particle, that is moved at a
single MC step. The probability 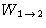 is the product of
is the product of
- 1.
- probability to pick particle 1, and the displacement vector,
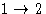 , equal to
, equal to 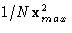 , and
, and
- 2.
- probability to accept the move by the Metropolis criterium,
equal to
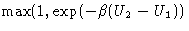
The probability of the opposite step 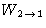 is the product of
is the product of
- 1.
- probability to pick particle 2, and the displacement vector
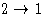 , equal to
, equal to 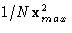 , and
, and
- 2.
- probability to accept the move by the Metropolis
criterium
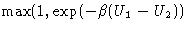
If the state 1 has higher energy than 2, then
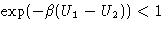 , and
, and 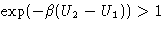 , the first
contributions are the same in both direct and reverse probabilities,
and equation 2 is satisfied.
, the first
contributions are the same in both direct and reverse probabilities,
and equation 2 is satisfied.
© 1997
Boris Veytsman
and Michael Kotelyanskii
Tue Nov 11 18:36:02 EST 1997
![]()
![]()
![]()
![]() is the product of
is the product of
![]() , and
, and ![]() , the first
contributions are the same in both direct and reverse probabilities,
and equation 2 is satisfied.
, the first
contributions are the same in both direct and reverse probabilities,
and equation 2 is satisfied.