


Next: Ideal Gas
Up: Systems with Many Particles.
Previous: Systems with Many Particles.
Subsections
Suppose we have N identical particles 1, 2,.... We
want to describe their thermodynamics--i. e. calculate
partition function.
- Mixtures:
- N1 particles of kind 1, N2 particles of kind
2, ....
- General formula:
- Gibbs law
| 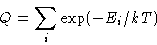 |
(1) |
What is a state in this formula?
- Quantum Answer:
- I have a number of quantum states for each
particle. The state is the set of occupation numbers n1,
n2, ...
- Consequence:
- For quantum mechanics the grand canonical ensemble
and
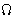 potential are more natural than canonical
ensemble and free energy!
potential are more natural than canonical
ensemble and free energy!
- Classical Answer:
- I need coordinate qi and momentum pi
for each of my particles plus information about the internal
degrees of freedom
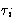 for each particle.
for each particle.
We will discuss only classical case.
- Kinetic energy. In the non-relativistic case it depends
only on the momenta:
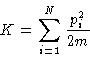
- Potential energy. In the classical case it depends only on
the coordinates:
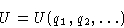
- Internal energy. Depends on the internal degrees of freedom
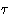 (often they are quantum--even if everything else is
classical!):
(often they are quantum--even if everything else is
classical!):
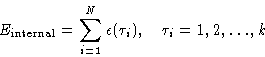
- Boltzmann principle:
- If the particles are identical,
exchanging them will not change the state. This is a
consequence of Quantum Mechanics.
For distinguishable particles classical partition function is:
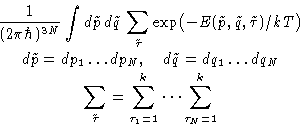
However, they are identical. States are overcounted--divide by
the number of permutations:
| 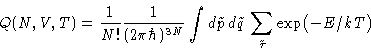 |
(2) |
This is called Boltzmann Statistics
Since
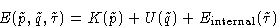
we can write:
| 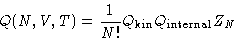 |
(3) |
- Kinetic part
-
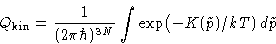
- Internal part
-
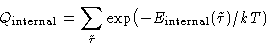
- Configuration integral
-
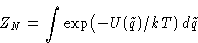
- 1.
- Large quantum effects: we must include them honestly instead of
as a kludge! But the kludge works for large temperatures (if
the distance between quantum levels is
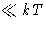 )
) - 2.
- Relativistic effects: at velocities about light speed
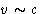 or high gravitation fields we cannot separate kinetic and potential
energy!
or high gravitation fields we cannot separate kinetic and potential
energy!
- 3.
- Polarisability: sometimes we cannot separate U and
 .
.
- 4.
- In non-Cartesian coordinates K might depend both on
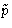 and
and 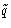 --we cannot separate it! In the systems with rigid
bonds we must use non-Cartesian coordinates.
--we cannot separate it! In the systems with rigid
bonds we must use non-Cartesian coordinates.
Since
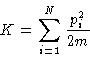
the kinetic part is fully factorizable:
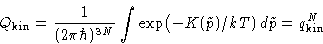
with
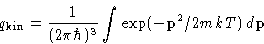
Vector momentum 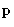 :
:
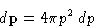
and
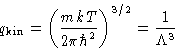
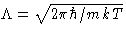 has the dimension of length. It is
called thermal de Brogile wavelength.
has the dimension of length. It is
called thermal de Brogile wavelength.
- Quantum interpretation:
- particles have wavelengths
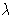 depending on the momentum p. Thermal wavelength
depending on the momentum p. Thermal wavelength 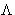 corresponds
to
corresponds
to 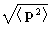 .
. - Validity of Boltzmann Distribution:
- Classical formulae work if
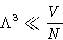
Since partition function is factorized, the probability to have
momentum 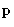
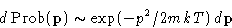
For velocity 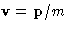
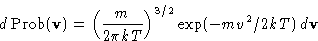
or, since 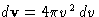
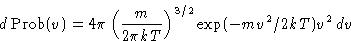
This is called Maxwell distribution
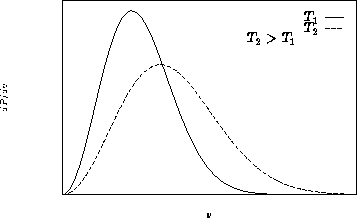
Average velocity
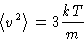
Average kinetic energy per molecule:
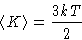
Another definition of temperature: in classical systems measures
the average kinetic energy of thermal motion.
In classical systems kinetic part can be separated from
other parts and calculated exactly!
The exact value depends on the molecular structure.
It is always factorizable:
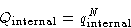
with
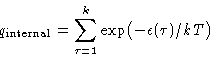
and  depends only on T!
depends only on T!
The kinetic part is calculated exactly--for all classical systems.
Calculation of the internal part is mostly a Quantum Mechanics problem.
Classical Statistical Thermodynamic is about calculation of the
configuration integral
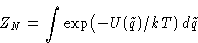



Next: Ideal Gas
Up: Systems with Many Particles.
Previous: Systems with Many Particles.
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Sep 17 22:58:45 EDT 1997
![]()
![]()
![]()
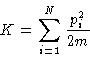
![]()
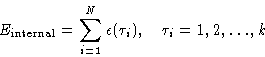
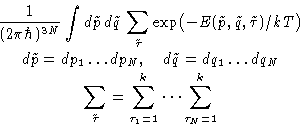
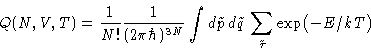
![]()
![]()
![]()
![]()
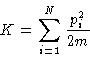
![]()
![]()
![]() :
:
![]()
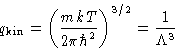
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
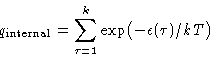
![]()