


Next: Quiz
Up: Systems with Many Particles.
Previous: Many-Particle Systems
Subsections
- Definition:
- Ideal Gas is the system where interaction is absent
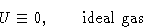
- Configuration Integral:
- This is factorizable!
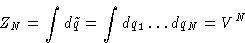
- Partition Function:
-

Let us calculate 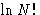 for
for  :
:
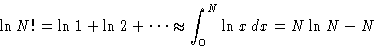
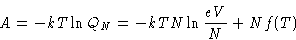
with
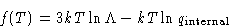
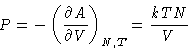
Pressure of ideal gas does not depend on the nature of the gas!
Entropy:
| 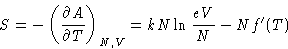 |
(4) |
or, substituting V by NkT/P
| 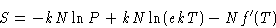 |
(5) |
Heat capacity:
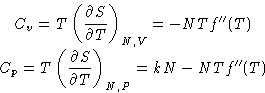
We obtained:
Cp-Cv = kN
|
E = A+TS = Nf(T)-NTf'(T)
|
(6) |

Suppose we have a container of the volume 2V with 2N particles,
divided into two parts. We deleted the divider. What
is the entropy change?
- First Method:
- Let us paint the particles in the left in white,
and particle in the right in black. After we deleted the divider,
``white'' and ``black'' particles mix. From equation (4) the
change of entropy for ``white particles'' is
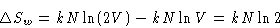
For ``black particles'' 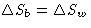 . Total change of
entropy is
. Total change of
entropy is
| 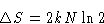 |
(7) |
- Second Method:
- Entropy is an extensive variable, so the entropy for
2N molecules in the volume 2V is twice the entropy for N
molecules in the volume V
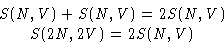
and
| 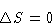 |
(8) |
What is wrong? Why we obtained different answers?
- Solution:
- The distinguishability is a quantum effect: it
is either there, or not (particles cannot be a little bit
different!). If they are identical, we cannot speak about entropy
of white or black particles separately--and only (8)
works. If they are not identical, only (7) works.
- Consequence:
- There is an entropy change when mixing different
isotopes--even while the molecules are quite similar!



Next: Quiz
Up: Systems with Many Particles.
Previous: Many-Particle Systems
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Sep 17 22:58:45 EDT 1997
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
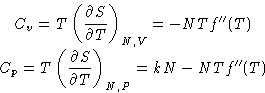

![]()
![]()