Van der Waals Equation

We know that liquids are (almost) incompressible. So A(N,V,T) should diverge at $V\sim Nb$. How can we arrange this?

Start from virial equation:
$$\begin{multline*} A=A_{\text{ideal}} + \frac{N^2kTB(T)}{V} =\ -kTN\ln\frac{eV}{N} + Nf(T) + \frac{N^2kTb}{V} - \frac{N^2a}{V}\end{multline*}$$
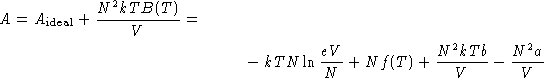
Rearrange the terms:  

$$A = Nf(T)-NkT\ln\frac{e}{N} -NkT\left(\ln V-\frac{N b}{V}\right) - \frac{N^2a}{V}$$ (8)

We want an equation, that:

• Has the same behavior at $V\gg Nb$
• Diverges at $V\sim Nb$.

Idea: substitute $\ln V - Nb/V$ by $\ln(V-Nb)$.

• At $V\gg Nb$

  $$\ln(V-Nb) = \ln V + \ln\left(1-\frac{Nb}{V}\right)\approx \ln V - \frac{Nb}{V}$$

• At $V\sim Nb$

  $$\ln(V-Nb)\to\infty$$

Result: van der Waals formula  

$$A = Nf(T)-NkT\ln\frac{e}{N} -NkT\ln \left(V-N b\right) - \frac{N^2a}{V}$$ (9)

Pressure:

$$P= -\left(\frac{\partial A}{\partial V}\right)_{N,T} = \frac{NkT}{V-Nb} - \frac{N^2a}{V^2}$$

At $V\to Nb$ it diverges.